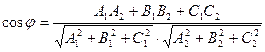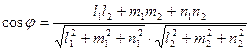Глоссарий

№ п/п	Новое понятие	Содержание
1	2	3
1	Общее уравнение плоскости	Уравнение вида , где , линейное относительно x, y, z - координат произвольной (текущей) точки плоскости
2	Вектор нормали к плоскости	Ненулевой вектор , перпенди-кулярный к данной плоскости
3	Уравнение плсокости, проходящей через точку , с данным вектором нормали	Уравнение , (x, y, z) - текущая точка плоскости
4	Уравнение плоскости, проходящей через три заданные точки , и	Уравнение , являющиеся условием компланарности векторов , и
5	Формула для вычисления расстояния D от точки до плоскости
6	Условие параллельности двух плоскостей и	, определяющее параллельность (коллинеарность) векторов нормали и
7	Условие перпендикулярности двух плоскостей и	, определяющее ортогональность векторов нормали и
8	Каноническое уравнение прямой	Уравнение вида , где - фиксированная (данная) точка на прямой, - текущая точка прямой, - направляющий вектор прямой
9	Параметрические уравнения прямой	Уравнения вида , где - данная точка на прямой, - текущая точка прямой, - направляющий вектор прямой, t - параметр
10	Прямая, как пересечение двух неколлинеарных плоскостей	, где векторы и не коллинеарны
11	Условие параллельности двух прямых и	Равенство , означающее коллине-арность направляющих векторов и
12	Условие перпендикулярности прямых и	Равенство , означа-ющее ортогональность направляющих векторов и
13	Угол между прямой и плоскостью	Угол между прямой L и ее проекцией на плоскость , синус которого вычисляется по формуле
14	Условие параллельности прямой и плоскости	Равенство =0, означающее ортогональность векторов и
15	Условие перпендикулярности прямой и плоскости	Равенства , означающее коллинеар-ность векторов и
16	Условие пересечения двух прямых и	Равенство , означающее компланарность векторов , и
17	Каноническое уравнение поверхностей второго порядка эллипсоида	Уравнение вида , где - положительные числа, полуоси эллипсоида
18	Каноническое уравнение поверхностей второго порядка - гиперболоидов	Однополостный гиперболоид - ; двуполостный гиперболоид -
19	Канонические уравнения поверхностей второго порядка - параболоидов	Эллиптический параболоид - (, ); гиперболический параболоид - (, )
20	Каноническое уравнение поверхностей второго порядка конуса	, , ,
21	Цилиндр второго порядка	Поверхность, в уравнении которой отсутствует одна из координат; направляющей цилиндра служит кривая второго порядка, а образующая параллельна той координатной оси, координата которой отсутствует в уравнении цилиндра
1	2	3
22	Линейчатая поверхность	Поверхность, через каждую точку которой проходит прямая, целиком принадлежащая этой поверхности
23	Поверхность вращения	Множество точек, которое образуется при вращении некоторой плоской линии L вокруг оси l (например, вокруг одной из координатных осей OX, OY, OZ)
24	Уравнение плоскости «в отрезках»	Уравнение плоскости, записанное в виде , Где числа a, b, c равны величинам отрезков, которые отсекает плоскость на осях OX, OY и OZ, соответственно (отрезки отсчитываются от начала координат)
25	Угол между двумя плоскостями и	Угол между нормальными векторами и ,
26	Угол между прямыми и	Угол между направляющими векторами и
27	Условия принадлежности прямой к плоскости	Равенства И =0, первое равенство означает, что точка , через которую проходит прямая, принадлежит плоскости, а вторая есть условие параллельности прямой и плоскости
28	Горловое сечение однополостного гиперболоида	Это горловой эллипс , который получается при сечении гиперболоида плоскостью OXY
29	Меридиан	Плоская кривая L, которая вращается вокруг одной из координатных осей
30	Ось вращения	Ось, вокруг которой вращается меридиан
31	Эллипсоид	Поверхность, каноническое уравнение которой имеет вид:
32	Двуполостный гиперболоид	Поверхность, задаваемая каноническим уравнением

< Предыдущая		Следующая >