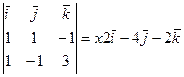Тренинг умений
Пример выполнения упражнения тренинга на умение 1а
Задание
Определите, лежит ли точка ![]() на плоскость
на плоскость ![]() .
.
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
В уравнение плоскости подставить вместо текущих координат x, y, z координаты точки |
|
|
2 |
Если при этом получится тождество, то точка |
Получили тождество, точка |
Выполните самостоятельно следующие задания:
Задание 1
Проходит ли плоскость ![]() через точку
через точку ![]() ?
?
Задание 2
Убедитесь, что расстояние от точки ![]() до плоскости
до плоскости ![]() , равно нулю (точка лежит на плоскости).
, равно нулю (точка лежит на плоскости).
Задание 3
Проходит ли плоскость ![]() через начало координат?
через начало координат?
Задание 4
Принадлежит ли точка ![]() плоскости
плоскости ![]() ?
?
Задание 5
Определить, какая из точек ![]() или
или ![]() лежит на плоскости
лежит на плоскости ![]() .
.
Пример выполнения упражнения тренинга на умение 1б
Задание
Найдите координаты какой-нибудь точки, лежащей на плоскости ![]() .
.
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Двум координатам из трех следует придать произвольные значения; если все три коэффициента |
Пусть |
|
2 |
Подставить выбранную пару координат в уравнении плоскости. |
|
|
3 |
Из полученного равенства найти третью координату. Замечание: если в уравнении плоскости отсутствует какая-либо из координат, то этой координате и одной из оставшихся присваиваются произвольные значения |
Точка (0,-1,-1) лежит на заданной плоскости. |
Выполните самостоятельно следующие задания:
Задание 1
Найдите какую-нибудь точку на плоскости ![]() .
.
Задание 2
Найдите какую-нибудь точку на плоскости ![]() .
.
Задание 3
Найдите какую-нибудь точку на плоскости ![]() .
.
Задание 4
Найдите какую-нибудь точку на плоскости ![]() .
.
Задание 5
Найдите какую-нибудь точку на плоскости ![]() .
.
Пример выполнения упражнения тренинга на умение 2
Задание
Найдите нормальный вектор ![]() к плоскости, в которой лежат векторы
к плоскости, в которой лежат векторы ![]() и
и ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Проверить, будут ли векторы |
Условие коллиеарности не выполнено, задача имеет единственное решение |
|
2 |
Найти векторное произведение |
|
|
3 |
Положить вектор |
|
Выполните самостоятельно следующие задания:
Задание 1
Найдите вектор нормали к координатной плоскости XOZ.
Задание 2
Найдите вектор нормали ![]() к плоскости, проходящей через три точки
к плоскости, проходящей через три точки ![]() ,
, ![]() и
и ![]() .
.
Задание 3
Найдите вектор нормали к плоскости, параллельной плоскости XOY.
Задание 4
Найдите вектор нормали к плоскости, параллельной векторам ![]() и
и ![]() .
.
Задание 5
Найти вектор нормали к плоскости, в которой лежат векторы ![]() и
и ![]() .
.
Пример выполнения упражнения тренинга на умение 3
Задание
Найти расстояние от точки ![]() до плоскости
до плоскости ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Вычислить расстояние d по формуле
|
Точка |
Выполните самостоятельно следующие задания:
Задание 1
Найдите расстояние от точки ![]() до плоскости
до плоскости ![]() .
.
Задание 2
Найдите расстояние от точки![]() до плоскости
до плоскости ![]() .
.
Задание 3
Найдите расстояние от точки ![]() до плоскости XOZ.
до плоскости XOZ.
Задание 4
Найти расстояние от начала координат до плоскости ![]() .
.
Задание 5
Найти расстояние между двумя параллельными плоскостями ![]() и
и ![]() . (Указание: использовать умение 3).
. (Указание: использовать умение 3).
Пример выполнения упражнения тренинга на умение 4а
Задание
Напишите каноническое уравнение прямой, проходящей через точки ![]() и
и ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Вычислить координаты вектора |
|
|
2 |
Взять направляющий вектор |
|
|
3 |
Написать каноническое уравнение прямой с направляющим вектором |
|
Выполните самостоятельно следующие задания:
Задание 1
Напишите уравнение прямой, проходящей через две точки ![]() и
и ![]()
Задание 2
Напишите уравнение прямой, проходящей через две точки ![]() и
и ![]() .
.
Задание 3
Напишите уравнение прямой, проходящей через две точки ![]() и
и ![]() .
.
Задание 4
Напишите уравнение прямой, проходящей через две точки ![]() - начало координат,
- начало координат, ![]() .
.
Задание 5
Написать уравнение оси OY, выбрав на ней произвольные две точки.
Пример выполнения упражнения тренинга на умение 4б
Задание
Написать параметрические уравнения прямой ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Обозначить коэффициент пропорциональности через t |
|
|
2 |
Из полученных равенств выразить координаты x, y, z |
Параметрические уравнения данной прямой |
Выполните самостоятельно следующие задания:
Задание 1
Напишите параметрические уравнения прямой ![]() .
.
Задание 2
Напишите параметрические уравнения прямой ![]() .
.
Задание 3
Напишите параметрические уравнения прямой ![]() .
.
Задание 4
Напишите параметрические уравнения прямой ![]() .
.
Задание 5
Напишите параметрические уравнения прямой ![]() .
.
Пример выполнения упражнения тренинга на умение 5
Задание
Написать каноническое уравнение прямой, заданной как пересечение двух плоскостей ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Найти какую-нибудь точку |
Пусть
Т. к. |
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
2 |
Выписать координаты векторов нормали |
|
|
3 |
Найти векторное произведение |
|
|
4 |
Взять направляющим вектором прямой вектор |
|
|
5 |
Выписать каноническое уравнение прямой |
|
Замечание. В данной задаче направляющий вектор ![]() может быть получен так:
может быть получен так:
1. Найти две различные точки ![]() и
и ![]() на данной прямой.
на данной прямой.
2. ![]() =
= ![]() .
.
В рассмотренном примере: точка ![]() (0,-1,0), а при
(0,-1,0), а при ![]() =1 получаем точку
=1 получаем точку ![]() (-1,1,1), и
(-1,1,1), и ![]()
![]() .
.
Выполните самостоятельно следующие задания:
Задание 1
Напишите каноническое уравнение прямой ![]() .
.
Задание 2
Напишите каноническое уравнение прямой ![]() .
.
Задание 3
Напишите каноническое уравнение прямой ![]() .
.
Задание 4
Напишите каноническое уравнение оси ОХ (как пересечение координатных плоскостей).
Задание 5
Напишите каноническое уравнение прямой пересечения плоскости ![]() с координатной плоскостью XOY.
с координатной плоскостью XOY.
Пример выполнения упражнения тренинга на умение 6
Задание
Найдите точку пересечения прямой ![]() с плоскостью
с плоскостью ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Записать параметрические уравнения прямой |
|
|
2 |
Полученные выражения для координат подставить в уравнение плоскости. |
|
|
3 |
Из полученного уравнения найти |
|
|
4 |
Подставить значение |
|
Выполните самостоятельно следующие задания:
Задание 1
Найдите точку пересечения плоскости ![]() с прямой L:
с прямой L: ![]() и
и ![]() .
.
Задание 2
Найдите точку пересечения плоскости ![]() с прямой L:
с прямой L: ![]() и
и ![]() .
.
Задание 3
Найдите точку пересечения плоскости ![]() с прямой L:
с прямой L: ![]() и
и ![]() .
.
Задание 4
Найдите точку пересечения плоскости ![]() с прямой L:
с прямой L: ![]() и
и ![]() - ось ОХ.
- ось ОХ.
Задание 5
Найдите точку пересечения плоскости ![]() с прямой L:
с прямой L: ![]() - плоскость XOZ и
- плоскость XOZ и ![]() .
.
Пример выполнения упражнения тренинга на умение 7
Задание
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
В выражениях |
Подставим в данное уравнение и получим |
|
2 |
Выписать преобразование коор-динат при параллельном сдвиге системы координат |
|
|
3 |
Подставить полученные выражения в уравнение поверхности и получить ее каноническое уравнение |
|
|
4 |
По каноническому уравнению определить тип поверхности и ее параметры |
Получили каноническое уравнение трехосного эллипсоида с центром симметрии в точке |
Выполните самостоятельно следующие задания:
Задание 1
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Задание 2
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Задание 3
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Задание 4
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Задание 5
Определите тип поверхности второго порядка и ее основные параметры по общему уравнению ![]() .
.
Пример выполнения упражнения тренинга на умение 8
Задание
По каноническому уравнению цилиндра ![]() определить: а) уравнение направляющей;
определить: а) уравнение направляющей;
б) какой координатной оси параллельны его образующие.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие |
|
1 |
Уравнение направляющей совпадает с уравнением цилиндра |
|
|
2 |
Образующие параллельны той коор-динатной оси, «название» которой в уравнении цилиндра отсутствует |
В уравнении отсутствует y, значит образующая параллельна оси OY |
|
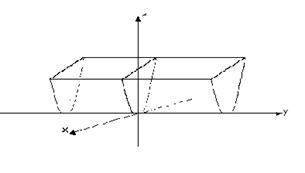
3 |
Построить чертеж |
|
Выполните самостоятельно следующие задания:
Задание 1
По каноническому уравнению цилиндра ![]() определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
Задание 2
По каноническому уравнению цилиндра ![]() определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
Задание 3
По каноническому уравнению цилиндра ![]() определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
Задание 4
По каноническому уравнению цилиндра ![]() определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
Задание 5
По каноническому уравнению цилиндра ![]() определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
определите: а) уравнение направляющей; б) какой координатной оси параллельны его образующие.
| < Предыдущая |
|---|
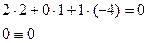
 лежит на плоскости
лежит на плоскости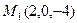 принадлежит данной плоскости
принадлежит данной плоскости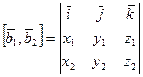
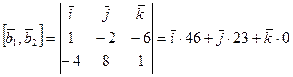


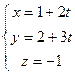
 , то система имеет единственное решение
, то система имеет единственное решение