6. Гиперплоскость в пространстве Rn

Рассмотрим в качестве примера арифметическое линейное пространство ,

И введенное в скалярное произведение векторов:

, где и , .

Пусть в задан некоторый ненулевой вектор , тогда функция, заданная для всякого следующим образом

,

Очевидно является линейным функционалом.

Рассмотрим в множество векторов , ортогональных вектору а.

Определение:

Уравнение , или

(3)

Определяет гиперплоскость в , проходящую через начало координат (нулевая гиперплоскость). Легко проверить, что совокупность точек , лежащих на гиперплоскости (3), является подпространством пространства .

Множество

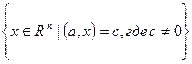
Также называют гиперплоскостью в , но это множество уже не образует подпространства, хотя бы потому, что не содержит 0-вектора.

В этом случае гиперплоскость является Сдвигом нулевой гиперплоскости

Вообще, если V - подпространство пространства , x0 – фиксированный вектор, не принадлежащий V, тогда совокупность W всех таких векторов x, что , где y пробегает все подпространство V, называют сдвигом подпространства V на вектор x0.

В этом многомерном случае легко видна аналогия с уравнением плоскости в трехмерном пространстве

, (4)

Где точка М с координатами (x, y, z) лежит на плоскости, а вектор

- вектор нормали к плоскости (4).

< Предыдущая		Следующая >