3. Поверхности второго порядка. 3.1. Общее уравнение второго порядка

Пусть в пространстве задана прямоугольная система координат OXYZ. Общим уравнением второго порядка (уравнением второй степени) относительно X, Y,Z называется уравнение вида

a11x2 + a22y2+a33z2+2a12xy+2a13xz+2a23yz+2a14x+2a24y+2a34z+a44=0, (23)

Где aij(i, j=1,2,3,4) – некоторые фиксированные числа (коэффициенты данного уравнения). Значения коэффициентов могут быть любыми, но при условии, что , , , , , одновременно не обращаются в нуль.

Поверхность второго порядка есть геометрическое место точек пространства, декартовы координаты которых удовлетворяют уравнению (23). В зависимости от коэффициентов в уравнении (23) поверхности второго порядка бывают вырожденными и невырожденными.

Приведем примеры вырожденных поверхностей второго порядка.

Пример 1. Пара пересекающихся плоскостей: , здесь =1, =-1, остальные коэффициенты равны нулю. Представим уравнение в виде (а) х = 0 или
(б) х - 2у = 0. Уравнение х = 0 – координатная плоскость УОZ, уравнение х – 2у = 0 задает плоскость, проходящую через ось OZ. По этой оси обе плоскости пересекаются.

Пример 2. Пара параллельных плоскостей: =1, , остальные коэффициенты =0. Представим уравнение в виде или . Плоскость является координатной ZОУ, плоскость параллельна ей.

Пример 3. Единственная точка: . Уравнению удовлетворяет единственная точка – начало координат.

Пример 4. Пустое множество: . Очевидно, ни одна точка пространства не удовлетворяет этому уравнению.

В дальнейшем мы подробно рассмотрим невырожденные поверхности второго порядка, к ним относятся эллипсоид, гиперболоид, параболоид, конус и цилиндры. Свойства поверхностей второго порядка не зависят от выбора декартовой системы координат. Вид уравнения поверхности существенно зависит от выбора системы координат.

В левую часть уравнения (23) входит функция трех переменных

,

Которая называется квадратичной формой от переменных ,,, а матрица

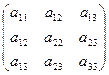
Называется матрицей квадратичной формы. Она симметрична, т. к. совпадают коэффициенты, расположенные симметрично относительно главной диагонали. Определитель этой матрицы играет важную роль при определении типа поверхности, заданной общим уравнением.

Кроме того, левая часть уравнения (23) содержит линейную функцию трех переменных

.

< Предыдущая		Следующая >