3.2. Канонические уравнения второго порядка

Можно выбрать такую систему координат ОХУZ, в которой уравнение поверхности имеет «наиболее простой» вид: в квадратичной форме отсутствуют члены с произведением координат, а линейная форма содержит лишь константу.

Такое уравнение поверхности второго порядка называется Каноническим уравнением этой поверхности.

Перечислим канонические уравнения поверхностей, которые мы далее будем изучать. А затем, по этим уравнениям определим форму некоторых поверхностей, используя для этого так называемый «метод параллельных сечений».

Канонические уравнения поверхностей второго порядка:

- Эллипсоид

- одНополостный гиперболоид

- Двуполостный гиперболоид

- эллиптический параболоид

- Гиперболический параболоид

- Конус

- Эллиптический цилиндр

- Гиперболический цилиндр

- Параболический цилиндр

Мы уже говорили, что введением соответствующей системы координат (преобразованием исходной) общее уравнение второго порядка можно привести к каноническому виду. В данном пособии мы не ставим задачи рассмотрения этих преобразований. Отметим лишь, что в некоторых случаях простым выделением полного квадрата (преобразованием параллельного сдвига) общее уравнение поверхности может быть приведено к каноническому виду.

Так, уравнение

Можно упростить следующим образом:

Или

.

Отсюда

.

Как и в плоском случае, преобразованием координат (параллельным сдвигом)

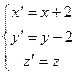
Получим каноническое уравнение эллипсоида в системе координат

.

< Предыдущая		Следующая >