3.5.4. Параболоиды
Пусть уравнение второго порядка приведено к каноническому виду ![]() ,
, ![]() ,
, ![]() . Поверхности, заданные этими уравнениями, называют параболоидами.
. Поверхности, заданные этими уравнениями, называют параболоидами.
Уравнение ![]() определяет эллиптический параболоид. Исследуя форму этой поверхности методом параллельных сечений, можно убедиться, что в сечении плоскостями, параллельными координатным, получаются либо параболы, либо эллипсы (отсюда и название поверхности). Таким образом поверхность имеет вид бесконечной выпуклой чаши с двумя взаимно перпендикулярными плоскостями симметрии, проходящими через начало координат (рис. 13).
определяет эллиптический параболоид. Исследуя форму этой поверхности методом параллельных сечений, можно убедиться, что в сечении плоскостями, параллельными координатным, получаются либо параболы, либо эллипсы (отсюда и название поверхности). Таким образом поверхность имеет вид бесконечной выпуклой чаши с двумя взаимно перпендикулярными плоскостями симметрии, проходящими через начало координат (рис. 13).
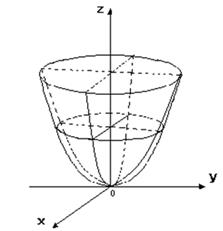
Рис. 13
Эллиптический параболоид, полученный вращением параболы ![]() вокруг оси Oz, имеет уравнение:
вокруг оси Oz, имеет уравнение:
![]() и является Параболоидом вращения.
и является Параболоидом вращения.
Гиперболический параболоид задается уравнением:
![]() ,
, ![]() ,
, ![]() .
.
В сечении этого гиперболоида плоскостями, параллельными координатным, получаются гиперболы и параболы (что и определяет название поверхности). Эта поверхность имеет форму седла (рис. 14). Гиперболический параболоид имеет две взаимно перпендикулярные плоскости симметрии, совпадающие с координатными плоскостями y = 0 (XOZ) и x = 0 (YOZ). Начало координат – вершина параболоида является ее «седловой» точкой».
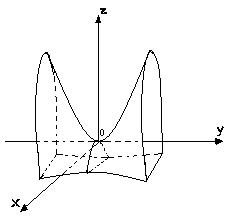
Рис. 14
| < Предыдущая | Следующая > |
|---|