3.5.3. Двуполостный гиперболоид
Поверхность, задаваемая каноническим уравнением
![]()
Называется Двуполостным гиперболоидом.
Величины ![]()
![]()
![]() положительны и называются полуосями двуполостного гиперболоида.
положительны и называются полуосями двуполостного гиперболоида.
1. Двуполостный гиперболоид - центральная поверхность с центром в начале координат; оси координат являются его осями симметрии, а координатные плоскости – плоскостями симметрии двуполостного гиперболоида.
2. Рассмотрим сечения этой поверхности координатными плоскостями. Сечение плоскостью XOZ задается уравнениями:
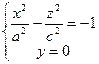
И представляет собой гиперболу, расположенную симметрично относительно координатных осей OX, OZ и пересекающую ось OZ в точках (0,0,с) и (0,0, - с).
Сечение плоскостью YOZ определяется уравнениями

и задает гиперболу, расположенную симметрично относительно осей OY и OZ и пересекающую ось OZ в точках (0,0,с) и (0,0, - с).
Рассмотрим теперь сечения данного гиперболоида плоскостями, параллельными координатной плоскости XOY (z = h), эти сечения задаются уравнениями
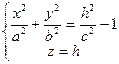 .
.
Отсюда видно, что при ![]() > c плоскость z = h пересекает двуполостный гиперболоид по эллипсу с полуосями
> c плоскость z = h пересекает двуполостный гиперболоид по эллипсу с полуосями ![]() ,
, ![]() , расположенному симметрично относительно плоскостей XOZ и YOZ; при возрастании
, расположенному симметрично относительно плоскостей XOZ и YOZ; при возрастании ![]() величины
величины ![]() ,
, ![]() возрастают; если
возрастают; если ![]() , убывая, приближается к
, убывая, приближается к ![]() , то
, то ![]() ,
, ![]() убывают, причем при
убывают, причем при ![]() имеем
имеем ![]() =0,
=0, ![]() =0; это означает, что эллипс, образуемый сечением плоскостью z = c, или z = - c, вырождается в точку, т. е. плоскости
=0; это означает, что эллипс, образуемый сечением плоскостью z = c, или z = - c, вырождается в точку, т. е. плоскости ![]() касаются гиперболоида; при
касаются гиперболоида; при ![]() <c сечения определяют мнимый эллипс, т. е. при
<c сечения определяют мнимый эллипс, т. е. при ![]() <c плоскость z=h не пересекается с двуполостным гиперболоидом.
<c плоскость z=h не пересекается с двуполостным гиперболоидом.
|
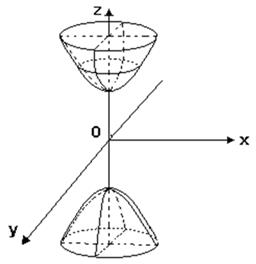
Рис. 12
| < Предыдущая | Следующая > |
|---|