3.5.2. Однополостный гиперболоид
Поверхность, задаваемая каноническим уравнением
![]()
Называется Однополостным гиперболоидом. Постоянные ![]()
![]()
![]() положительны и называются полуосями гиперболоида.
положительны и называются полуосями гиперболоида.
1. Как и эллипсоид, эта поверхность центральная с центром симметрии в начале координат; оси координат являются осями симметрии, а координатные плоскости – плоскостями симметрии однополостного гиперболоида.
2. Рассмотрим сечения гиперболоида координатными плоскостями XOZ и YOZ. Сечение плоскостью XOZ задается уравнениями
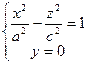 ,
,
Определяющими гиперболу, расположенную симметрично относительно координатных осей OX, OZ и пересекающую ось OX в точках ![]() ,
, ![]() .
.
Сечение плоскостью YOZ определяется уравнениями
 ,
,
задающими гиперболу, расположенную симметрично относительно координатных осей OY, OZ и пересекающую ось OY в точках ![]() ,
, ![]() .
.
Рассмотрим теперь сечение гиперболоида плоскостями z = h. Эти сечения определяются уравнениями
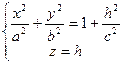 .
.
Отсюда видно, что любая плоскость z = h пересекает гиперболоид по эллипсу с полуосями
![]() ,
, ![]() ,
,
Расположенному симметрично относительно плоскостей XOZ и YOZ; величины ![]() ,
, ![]() имеют наименьшее значение при h = 0, иначе говоря, самых малых размеров эллипс получается в сечении координатной плоскостью XOY (z = 0), этот эллипс называется Горловым сечением однополостного Гиперболоида, его уравнение имеет вид
имеют наименьшее значение при h = 0, иначе говоря, самых малых размеров эллипс получается в сечении координатной плоскостью XOY (z = 0), этот эллипс называется Горловым сечением однополостного Гиперболоида, его уравнение имеет вид ![]() ; при возрастании
; при возрастании ![]() значения
значения ![]() И
И ![]() бесконечно возрастают.
бесконечно возрастают.
Сопоставляя изложенное, можно сказать, что однополостный гиперболоид имеет вид бесконечной трубки, бесконечно расширяющейся в обе стороны от горлового сечения. Этот гиперболоид имеет три плоскости симметрии, при данном выборе системы координат эти плоскости совпадают с координатными плоскостями XOY, XOZ, YOZ (рис. 11)
При ![]() =
=![]() однополостный гипербо-лоид превращается в гиперболоид враще-ния
однополостный гипербо-лоид превращается в гиперболоид враще-ния ![]() , он может быть получен вращением гиперболы
, он может быть получен вращением гиперболы ![]() , вокруг оси OZ.
, вокруг оси OZ.

Рис. 11.
| < Предыдущая | Следующая > |
|---|