3.5.1. Эллипсоид
Эллипсоидом называют поверхность, каноническое уравнение которой имеет вид:
,
Где 
- положительные числа, называемые полуосями эллипсоида.
Исследуем форму этой поверхности.
1. Координаты 
в каноническое уравнение входят во второй степени, следовательно, координатные плоскости являются плоскостями симметрии, а координатные оси – осями симметрии эллипсоида; заметим, что вместе с точкой 
поверхности принадлежит и точка 
, т. е. начало координат является Центром симметрии Поверхности – эллипсоид относится к центральным поверхностям.
2. Из канонического уравнения следует, что 
, 
, 
, или 
для всех точек эллипсоида, т. е. эллипсоид целиком располагается внутри параллелепипеда с ребрами 
, т. е. эллипсоид - ограниченная поверхность.
3. Применим метод параллельных сечений.
Рассмотрим сечение эллипсоида координатной плоскостью ОХУ (z=0) и плоскостями 
.
В сечении получатся эллипсы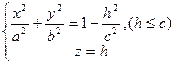
.
Полуоси эллипсов пересечения 
имеют наибольшие значения в плоскости ХОУ при h=0, при возрастании h значения 
убывают и обращаются в нуль при 
. Это означает, что плоскости 
имеют по одной общей точке с эллипсоидом, являются касательными плоскостями.
Аналогичные заключения можно сделать, рассекая эллипсоид плоскостями, параллельными ХОZ и УОZ. В частности, при пересечении эллипсоида плоскостями ХОZ (у=0) и УОZ (х=0) в сечении получаются эллипсы 
и 
. Суммируя проведенные исследования, приходим к выводу, что в данной системе координат эллипсоид имеет вид (рис. 10):
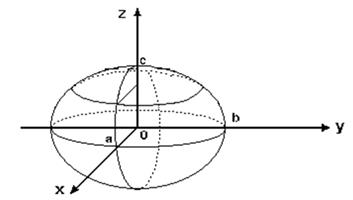
Рис. 10
Итак, эллипсоид есть замкнутая овальная поверхность, обладающая тремя взаимно перпендикулярными плоскостями симметрии.
Если полуоси 
эллипсоида различны, эллипсоид называется Трехосным. Если же какие-либо две из величин одинаковы, например, 
= 
, тогда при пересечении с плоскостью получаются окружности 
с центром на оси OZ. Данный эллипсоид
Является Эллипсоидом вращения и получается при вращении эллипса вокруг оси OZ.
В случае, когда все полуоси равны = = получается сфера 
с центром в начале координат и радиусом 
.
| < Предыдущая | Следующая > |
|---|
