2.1.1. Прямая как пересечение двух неколлинеарных плоскостей
Рассмотрим две плоскости A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Пусть векторы – нормали этих плоскостей не коллинеарны, их координаты не пропорциональны, а значит не выполняется хотя бы одно из равенств
![]() .
.
Отсюда следует, что хотя бы один из трех определителей
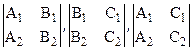 (13)
(13)
Отличен от нуля. Тогда данные плоскости пересекаются по прямой, уравнение которой имеет вид (такое уравнение прямой называют общим)
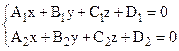 , (14)
, (14)
Где хотя бы один из определителей (13) не равен нулю. Заметим, что направляющий вектор ![]() прямой (14) ортогонален каждому из векторов
прямой (14) ортогонален каждому из векторов ![]() и
и ![]()
![]()
![]() ,
,
Откуда следует, что ![]() .
.
Поставим задачу: перейти от уравнения прямой (14) к её каноническому уравнению. Чтобы написать каноническое уравнение прямой, необходимо знать какую-нибудь точку на прямой и её направляющий вектор ![]() . Что касается направляющего вектора, то этим вектором может служить векторное произведение [
. Что касается направляющего вектора, то этим вектором может служить векторное произведение [![]() ,
,![]() ].
].
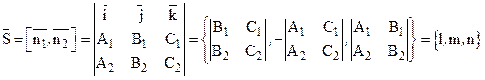 .
.
Чтобы определить какую-нибудь точку М0(x0,y0,z0) на прямой, следует выбрать одно частное решение из множества решений системы (14). Для этого достаточно применить одну из координат точки М0 равной нулю, так, если
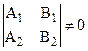 ,
,
То полагаем z0=0 и находим единственное решение системы
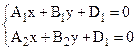 .
.
| < Предыдущая | Следующая > |
|---|