2. Прямая в пространстве. 2.1. Различные уравнения прямой
Рассмотрим прямую L в пространстве, проходящую через точку М0(x0,y0,z0) параллельно вектору ![]() =(l, m,n), который называют Направляющим. Пусть М(x, y,z) – произвольная (текущая) точка на прямой. Тогда (и только тогда) векторы
=(l, m,n), который называют Направляющим. Пусть М(x, y,z) – произвольная (текущая) точка на прямой. Тогда (и только тогда) векторы ![]() и
и ![]() коллинеарны, т. е.
коллинеарны, т. е.
![]() =t·
=t·![]() , (10)
, (10)
Где t – действительное число (параметр).
Распишем покоординатно уравнение (10):
![]()
![]()
![]() , или
, или
 (11)
(11)
Уравнения (11) называются Параметрическими уравнениями прямой L в пространстве. При любом t уравнения (11) определяют некоторую точку М(x, y,z) на прямой L и, обратно, для любой точки М на прямой L однозначно определяется значение параметра t. Уравнения (11) можно трактовать как уравнения равномерного движения точки М (x, y,z) по указанной прямой, а вектор ![]() (l, m,n) – вектор скорости движения точки. При t=0 получаем «начальную» точку M0(x0,y0,z0) (рис. 4).
(l, m,n) – вектор скорости движения точки. При t=0 получаем «начальную» точку M0(x0,y0,z0) (рис. 4).
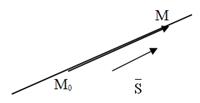
Рис. 4
Выразим параметр t из уравнений (11) и исключим его.
![]() , или
, или
![]() (12)
(12)
Уравнения (12) называют Каноническим уравнением прямой в пространстве. Фактически уравнения (12) выражают пропорциональность координат векторов ![]() и
и ![]() , т. е. условие коллинеарности этих векторов в координатной форме. Отметим, что в равенствах (12) содержится два линейных уравнения (третье следует из первых двух).
, т. е. условие коллинеарности этих векторов в координатной форме. Отметим, что в равенствах (12) содержится два линейных уравнения (третье следует из первых двух).
Может случиться, что какие-то координаты направляющего вектора ![]() равны нулю, этого не следует бояться. В каноническом уравнении допускается форма записи, например:
равны нулю, этого не следует бояться. В каноническом уравнении допускается форма записи, например:
![]() .
.
Эту запись следует понимать так, что вторая координата вектора ![]() равна нулю, y – 1 = 0, или
равна нулю, y – 1 = 0, или  , т. е. если знаменатель в (12) равен нулю, то и числитель – ноль.
, т. е. если знаменатель в (12) равен нулю, то и числитель – ноль.
| < Предыдущая | Следующая > |
|---|