1.1.3. Смешанное произведение

Определение. Смешанным произведением трех векторов , и называется число, обозначаемое :

=([,],)=(,[,])

Геометрический смысл смешанного произведения: если V – объем параллелепипеда, построенного на векторах , и , (рис. 1) то

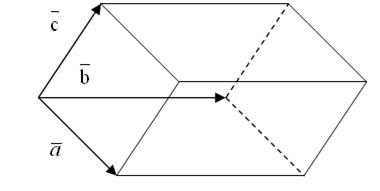
Рис. 1

Смешанное произведение в координатной форме Вычисляют так:

,

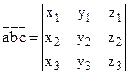Где =(x1,y1,z1), =(x2,y2,z2) и =(x3,y3,z3).

Из геометрического смысла следует условие компланарности трех векторов:

=0 ,, компланарны (лежат или параллельны одной плоскости).

< Предыдущая		Следующая >