1.1.2. Векторное произведение

Определение. Векторное произведение двух векторов и – это вектор , обозначаемый =[,] или =, такой что:

1) ;

2) и , т. е. векторное произведение перпендикулярно плоскости векторов и ;

3) ,, образуют правую тройку.

Координаты векторного произведения [,] через координаты сомножителей =(x1, y1, z1) и =(x2, y2, z2) вычисляют так:

,

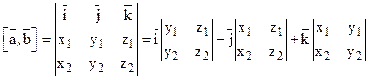Т. е. координатами [,] служат определители

.

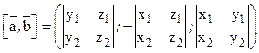Заметим, что численно равен площади параллелограмма, построенного на векторах и (следует из определения).

Отметим также, что

.

< Предыдущая		Следующая >