1. Плоскость в пространстве. 1.1. Элементы векторной алгебры. 1.1.1. Скалярное произведение

Определение. Скалярное произведение двух векторов и - число, обозначаемое (,) или и вычисляемое по формуле

(,) = •,

Где – длины векторов, φ – угол между и .

В координатной форме скалярное произведение векторов =(x1, y1, z1) и =(x2, y2, z2) вычисляют так:

(,)=х1·x2+y1·y2+z1·z2.

В частности, скалярный квадрат вектора (,)=.

Из определения скалярного произведения для ненулевых векторов следует, что

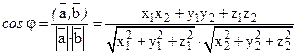
Отсюда следует, что векторы и ортогональны () тогда и только тогда, когда их скалярное произведение равно нулю:

.

Следующая >