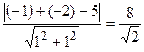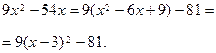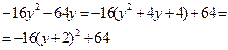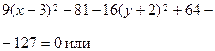3. Тренинг
1 Алгоритм формирования компетенций
|
Компетенция |
Этап формирования*. Алгоритм расчета |
|
Освоения методики использо-вания программных средств для решения практических задач (ПК-2) |
A. Написать уравнение прямой L, проходящей через точку M1(X1, Y1) и точку M2(X2, Y2), перпендикулярно прямой L1: A1X + B1Y + C1 = 0, параллельно прямой L2: A2X + B2Y + + C2 = 0. 1. Записать уравнение прямой 2. Использовать условие параллельности двух прямых и найти угловой коэффициент искомой прямой: 3. Написать уравнение прямой с угловым коэффициентом
|
|
B. Найти точку М пересечения прямых L1: L2: A2X + B2Y + C2 = 0 И вычислить расстояние от точки М до данной прямой L3: A3X + B3Y + C3 = 0. 1. Изучить тему «Уравнения прямой». 2. Найти координаты
3. Найти расстояние D от точки М(X1, Y1) до прямой L3:
| |
|
C. Найти угол пересечения прямых
А) для случая, когда прямые пересекаются, Б) для случая, когда прямые параллельны, В) для случая, когда прямые перпендикулярны. 1. Изучить тему «Уравнения прямых». 2. а) определить угол между прямыми L1 и L2 по формуле
Б) если В) признак перпендикулярности прямых
Знаменатель в формуле | |
|
Компетенция |
Этап формирования. Алгоритм расчета |
|
D. Определить тип кривой второго порядка по заданному общему уравнению (отсутствует произведение координат). Выписать ее параметры. 1. Ознакомиться с каноническими уравнениями кривых второго порядка. 2. Выделить полные квадраты независимых переменных. 3. Преобразовать уравнение к одному из следующих видов: A) B) C) Или
4. Определить тип кривой: если уравнение привели к виду а) – эллипс; к виду b) – гипербола; к виду с) – парабола. 5. Выписать параметры кривой из ее уравнения. Для эллипса и гиперболы: A) полуоси a И B; B) расстояние между фокусами 2С, где Координаты (Х0, У0) центра симметрии. Для параболы: A) координаты вершины (Х0, У0); Координаты фокуса: |
2 Формирование компетенций
ПК-2. Освоение методики использования программных средств для решения практических задач
Этап формирования ПК-2. А. Написать уравнение прямой L, проходящей через точку M1(X1, Y1) и точку M2(X2, Y2), перпендикулярно прямой L1: A1X + B1Y + C1 = 0, параллельно прямой L2: A2X + B2Y + + C2 = 0
Решение типовой задачи
Условие задачи
Даны вершины треугольника А(1, –1), В(0, 2), С(3, 1). Составить уравнения: 1), высоты АD;
2) медианы АЕ; 3) средней линии, параллельной стороне АС.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
1. Ознакомиться с основными способами задания прямой на плоскости. Подзадача 10 2а) Написать направляющий вектор прямой ВС:
3а) Написать каноническое уравнение прямой по точке и направляющему вектору. 2в) Выписать вектор нормали к прямой ВС. 3в) Выписать вектор 4в) Написать уравнение прямой АD по точке А и вектору нормали Подзадача 20: 2а) Написать каноническое уравнение медиа-ны АЕ по двум точкам А и Е (середина ВС) Подзадача 30: 2а) Выписать уравнение прямой АС По двум точкам А и С. 2с) Запишем уравнение прямой АС в виде У = Кх + B. 3с) Выписать условие параллельности прямой АС и искомой средней линии EF. 4с) Написать уравнение прямой EF по точке Е и угловому коэффициенту |
Решение подзадачи 10: 2а) Направляющий вектор прямой ВС бу-дет вектор 3а) уравнение прямой ВС:
2в) Вектор-нормаль 3в) 4в) Уравнение АD: –3(Х – 1) + 1(У + 1) = 0 или 3Х – у – 4 = 0. Решение подзадачи 20: 2а) Точка Е имеет координаты:
Каноническое уравнение АЕ:
(Х – 1)×2,5 = (У + 1)×0,5 или 5Х – у – 6 = 0. Решение подзадачи 30: 2а) Х – у – 2 = .0 2с) У = Х – 2, угловой коэффициент 3с) 4с) |
|
2 |
Задачи для самостоятельной работы
Задача 1
Даны вершины треугольника А(2, –2), В(3,-5), С(5,7). Составить уравнение высоты ВD и средней линии, параллельной АВ.
Задача 2
Составить уравнение всех сторон треугольника АВС, где А(3, 2), В(5, –2), С(5, 2).
Задача 3
Составить уравнение всех высот треугольника АВС, где А(3, 2), В(5, –2), С(1, 0).
Задача 4
Даны параллельные прямые 3Х – у + 2 = 0 и 3Х – у – 5 = 0. Написать уравнение прямой, им параллельной и проходящей на равном расстоянии от них.
Задача 5
Даны две смежные вершины А(–3, –1) и В(2, 2) параллелограмма АВСD и точка Q(3, 0) пересечения его диагоналей. Составить уравнение сторон этого параллелограмма.
Этап формирования ПК-2. В. Найти точку М пересечения прямых L1:![]() и L2: A2X + B2Y + C2 = 0 и вычислить расстояние от точки М до данной прямой L3: A3X + B3Y + C3 = 0
и L2: A2X + B2Y + C2 = 0 и вычислить расстояние от точки М до данной прямой L3: A3X + B3Y + C3 = 0
Решение типовой задачи
Условие задачи
Стороны АВ, ВС И СА треугольника АВС, соответственно, даны уравнениями: 3Х-у +1 = 0,
X+у-5 = 0, Х – 3У-5 = 0. Найти высоту, опущенную на сторону ВС.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Изучить тему «Уравнение прямой» | |
|
2 |
Найти координаты точки А пересечения прямых АВ И СА |
2. Найти решение системы
|
|
3 |
Найти расстояние D От точки А до стороны ВС |
3. Найти расстояние D от точки А(-1, –2) до стороны ВС: (Х + У - 5 = 0 –уравнение BC): D = |
|
4 |
Выписать ответ |
Длина искомой высоты равна |
Задачи для самостоятельной работы
Задача 1
Вычислить расстояние между параллельными прямыми 5Х – 12У + 26 = 0 и 5Х – 12У – 13 = 0.
Задача 2
Даны уравнения двух сторон прямоугольника 3Х – 2У – 5 = 0 и 2Х + 3У + 7 = 0 и одна из его вершин А(–2, 1). Вычислить площадь прямоугольника.
Задача 3
Доказать, что прямая 2Х – 3У + 6 = 0 не пересекает отрезок, ограниченный точками М1(–2, –3) и M2(1. –2).
Этап формирования ПК-2. С. Найти угол пересечения прямых ![]()
![]() а) для случая, когда прямые пересекаются, б) для случая, когда прямые параллельны, в) для случая, когда прямые перпендикулярны
а) для случая, когда прямые пересекаются, б) для случая, когда прямые параллельны, в) для случая, когда прямые перпендикулярны
Решение типовой задачи
Условие задачи
В прямоугольном треугольнике ABC заданы две стороны уравнениями ![]() и точка
и точка ![]() , принадлежащая обоим катетам. Найти уравнение третьей стороны треугольника AC и определить все углы треугольника.
, принадлежащая обоим катетам. Найти уравнение третьей стороны треугольника AC и определить все углы треугольника.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Изучить тему «Уравнения прямых» | |
|
2 |
Определить угол между прямыми AB и BC |
2.Определить угол Угол |
|
3 |
Определить, какой из прямых AB и BC принадлежит точка M? |
3. а) Подставим координаты точки M в уравнение прямой BC: Б) Подставим координаты точки M в уравнение прямой AB: |
|
4 |
Написать уравнение прямой AC. |
4. Т. к. AC – катет, AC перпендикулярна AB и |
|
5 |
Определить оставшиеся углы. |
|
Задачи для самостоятельной работы
Задача 1
Заданы координаты вершин треугольника ABC: ![]()
Написать уравнения сторон треугольника и определить его углы.
Задача 2
Заданы координаты вершин треугольника ABC:
![]()
Написать уравнения сторон треугольника и найти углы треугольника и его площадь.
Задача 3
Заданы координаты вершин параллелограмма ABCD:
![]()
Написать уравнения сторон параллелограмма и определить его углы.
Задача 4
Заданы координаты вершин параллелограмма ABCD:
![]()
Написать уравнения сторон параллелограмма и найти его площадь.
Задача 5
Заданы две параллельные прямые ![]() и
и ![]() и две различных точки
и две различных точки ![]() и
и ![]() на одной из прямых. Через заданные точки провести нормали к заданным прямым. Получится прямоугольник ABCD. Вычислить площадь прямоугольника и угол между его диагоналями.
на одной из прямых. Через заданные точки провести нормали к заданным прямым. Получится прямоугольник ABCD. Вычислить площадь прямоугольника и угол между его диагоналями.
Этап формирования ПК-2. D. Определить тип кривой второго порядка по заданному общему уравнению (отсутствует произведение координат). Выписать ее параметры
Решение типовой задачи
Условие задачи
Написать каноническое уравнение кривой 9X2 – 16Y2 – 54X – 64Y – 127 = 0. Определить тип кривой, выписать ее параметры.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Ознакомиться с каноническими уравнениями кривых второго порядка | |
|
2 |
Выделить полные квадраты независимых переменных |
|
|
3 |
Преобразовать уравнение |
|
|
4 |
Определить тип кривой |
Гипербола |
|
5 |
Выписать параметры кривой |
1. Действительная полуось A = 4, мнимая полуось B = 3. 2. 3. Центр симметрии С(3, –2). 4. Координаты фокусов: |
Задачи для самостоятельной работы
Задача 1
Привести к каноническому виду и определить тип кривой ![]() .
.
Задача 2
Привести к каноническому виду уравнение кривой ![]() . Определить ее тип и вычислить основные параметры.
. Определить ее тип и вычислить основные параметры.
Задача 3
Привести к каноническому виду уравнение кривой ![]() . Определить ее тип, вычислить основные параметры.
. Определить ее тип, вычислить основные параметры.
Задача 4
Привести к каноническому виду уравнение кривой ![]() . Определить ее тип, вычислить основные параметры.
. Определить ее тип, вычислить основные параметры.
Задача 5
Привести к каноническому виду уравнение второго порядка ![]() Определить тип кривой, вычислить основные параметры.
Определить тип кривой, вычислить основные параметры.
| < Предыдущая | Следующая > |
|---|
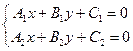 .
.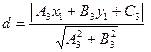 .
.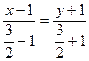 ;
;