2.7 Приведение кривой 2-го порядка к каноническому виду (с помощью выделения полного квадрата)

Рассмотрим случай, когда в общем уравнении (2.13) Отсутствует слагаемое с произведением координат, т. е. В = 0. Начнем с рассмотрения примера.

Пример 2.5. Привести к каноническому виду уравнение кривой

4X2 – 4X – Y2 + 2Y + 1 = 0.

Решение. Выделим полные квадраты:

4(X2 – X) – (Y2 – 2Y) + 1 = 0;

4((X – 0,5)2 – 0,25) – ((Y – 1)2 – 1) + 1 = 0;

4(X – 0,5)2 – 1 –(Y – 1)2 + 1 + 1 = 0

Или окончательно

Получили гиперболу с центром в точке (0,5;1), с действительной полуосью B = 1, мнимой полуосью А = 0,5.

Выделяя полные квадраты, исходное уравнение (2.13), где коэффициент В = 0, можно привести к одному из следующих видов (мы здесь опустим случай вырождения):

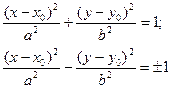
Или

(X – X0)2 = ±2P(Y – Y0),

(Y – Y0)2 = ±2P(X – X0).

Первые два уравнения определяют эллипс и гиперболы, центр симметрии которых находится в точке (X0, Y0), а оси симметрии параллельны осям координат.

Два последних уравнения – это параболы, вершина которых смещена из начала координат в точку (X0, Y0), а ось симметрии либо параллельна оси ОY, либо оси ОХ.

Введем теперь на плоскости новую систему координат ХОY (см. пунктир на рисунке 2.8), с новым началом координат в точке(X0, Y0) и осями ОХ, ОY, параллельными ОХ и ОY.

Произвольная точка М (Х, У) получит "новые координаты" М(Х, Y), причем связь между "новыми" и "старыми" координатами задается формулами:

X = X – X0 или X = X + X0;

Y = Y – Y0 или Y = Y + Y0. (2.15)

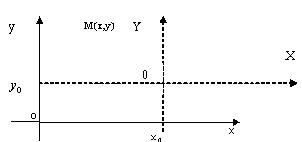
Рисунок 2.8

Такое преобразование системы координат называется Параллельным Переносом (сдвигом). В этой "новой" системе координат уравнения кривых примут уже знакомый нам канонический вид:

< Предыдущая		Следующая >