1.3.7 Расстояние от точки до прямой
Для вычисления расстояния D от точки М(X0, Y0) до прямой Ах + Ву + С = 0 используется Формула
. (1.20)
Приведем пример ее применения.
Пример 1.16. Найти расстояние между прямыми (L1) 2Х + 3У – 1 = 0 и(L2) 4Х + 6У + 5 = 0.
Решение. Векторы нормали данных прямых 
и 
коллинеарны 
, т. е. прямые параллельны. Выберем на прямой L1 фиксированную точку М(–1, 1), координаты которой удовлетворяют уравнению прямой (рисунок 1.10).
Воспользуемся теперь формулой (1.20) и вычислим расстояние от точки М1 до прямой L2:
Найденное расстояние является расстоянием между параллельными прямыми L1 и L2.
Задачу вычисления расстояния от данной точки до данной прямой Можно решить и другим способом, используя уже полученные знания.
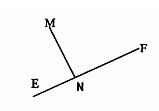
Пусть дана точка М(–1, 1) и прямая 3Х – 4У + 12 = 0. Необходимо найти расстояние от этой точки до прямой ЕF. Расстояние D от точки М до прямой EF равно длине перпендикуляра MN, опущенного из М на ЕF (рисунок 1.11).
Запишем алгоритм решения этой задачи.
1. Найдем угловой коэффициент К1 прямой EF, для этого разрешим уравнение прямой ЕF относительно У:
(1.21)
.
2. Используя условие перпендикулярности двух прямых, найдем угловой коэффициент K2 перпендикуляра MN:
Или 
, отсюда 
.
3. Теперь напишем уравнение прямой MN, проходящей через точку М(–1, 1) с угловым коэффициентом .
Или
(1.22)
4. Вычислим координаты точки N – точки пересечения прямой ЕF с перпендикуляром MN. Координаты этой точки удовлетворяют уравнениям (1.21) и (1.22), мы их получим, решив совместно эти уравнения. Приравняем правые части этих уравнений:
И вычислим отсюда абсциссу Х Точки N
или 
, откуда 
.
Подставив найденное значение, например, в уравнение (1.21), вычислим ординату точки N:
или 
, откуда 
.
Итак, точка N имеет координаты 
.
5. Найдем теперь расстояние между точками М и N:
.
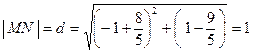Конечно, использованный выше алгоритм является достаточно громоздким. Он был приведен для того и продемонстрирован для того, чтобы показать различные способы решения задач такого типа.
Эту задачу можно легко решить, используя общую формулу вычисления расстояния D от точки М(Х0, У0) до прямой Ax + By + C = 0, которая была рассмотрена выше и имеет вид
(1.23)
Для нашей задачи мы получим
.
Разумеется, результаты, полученные различными способами, совпадают.
| < Предыдущая | Следующая > |
|---|
