08. Определенный интеграл как функция верхнего предела
Определение. Пусть функция F(T) определена и непрерывна на некотором промежутке, содержащем точку A. Тогда каждому числу X из этого промежутка можно поставить в соответствие число
![]()
Определив тем самым на промежутке функцию I(X), которая называется Определенным интегралом с переменным верхним пределом.
Отметим, что в точке X = a эта функция равна нулю.
Теорема. Производная определенного интеграла по верхнему пределу в точке X Равна значению подынтегральной функции в точке X.
Отсюда следует, что функция
![]()
Является первообразной для функции F(X), причем такой первообразной, которая принимает в точке X = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде
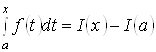 (1)
(1)
Пусть F(X) также является первообразной для функции F(X), тогда по теореме об общем виде всех первообразных функции
I(X)=F(X)+С,
где С — некоторое число. При этом правая часть формулы (1) принимает вид
![]() (2)
(2)
Из формул (1) и (2) после замены X На B Следует формула для вычисления определенного интеграла от функции F(T) по промежутку [A;B]
![]()
Которая называется Формулой Ньютона-Лейбница. Здесь F(X) — любая первообразная функции F(X).
Для того чтобы вычислить определенный интеграл от функции F(X) по промежутку [A;B], нужно найти какую-либо первообразную F(X) функции F(X) и подсчитать разность значений первообразной в точках B и A. Разность этих значений первообразной принято обозначать символом 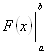 .
.
Пример. 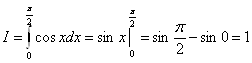 .
.
| < Предыдущая | Следующая > |
|---|