07. Определенный интеграл
Пусть на промежутке [A;b] задана функция F(X). Будем считать функцию непрерывной, хотя это не обязательно. Выберем на промежутке [A;b] произвольные числа ![]() , удовлетворяющие условию
, удовлетворяющие условию ![]() . Эти числа разбивают промежуток [A;B] на N более мелких промежутков [A;X1], [X1;X2],¼,[Xn-1;B]. На каждом из этих промежутков выберем произвольно по одной точке: C1Î[A;X1], c2Î[X1;X2],¼,CnÎ[Xn-1;B].
. Эти числа разбивают промежуток [A;B] на N более мелких промежутков [A;X1], [X1;X2],¼,[Xn-1;B]. На каждом из этих промежутков выберем произвольно по одной точке: C1Î[A;X1], c2Î[X1;X2],¼,CnÎ[Xn-1;B].
Введем обозначения
DX1=X1–A, DX2=X2–X1,¼,DXn=B–xn-1.
Составим сумму
![]() .
.
Эта сумма называется Интегральной суммой функции F(X) по промежутку [A;B]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек Ci.
Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника. Введем обозначение
L=Max(DXi), I=1,2,¼,N..
Величину L иногда называют Параметром разбиения. Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина L стремится к нулю.
Определение. Определенным интегралом 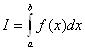 от функции
от функции ![]() по промежутку [A; B] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует
по промежутку [A; B] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует
![]() .
.
Если такой предел существует, то он не зависит от первоначального разбиения промежутка [A;B] на элементарные промежутки и от выбора точек Ci в них.
Число A Называется Нижним пределом интегрирования, а число B ¾ Верхним пределом интегрирования.
Свойства определенного интеграла:
1. 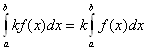 , где
, где ![]() ,
,
2. 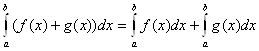 ,
,
3. 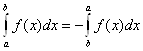 ,
,
4. если CÎ[A;B], то. 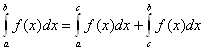 .
.
| < Предыдущая | Следующая > |
|---|