06. Интегрирование некоторых иррациональных функций

1. Интегралы вида , где R – рациональная функция, аргументами которой являются X и рациональные степени X .Для вычисления таких интегралов необходимо сделать подстановку X=Tk, где K -– наименьший общий знаменатель дробей .

Пример 1.

2. Интегралы вида .

Выделим в квадратном трёхчлене полный квадрат, получим

Таким образом, сведём данный радикал к радикалу одного из трёх видов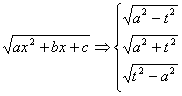

После чего используем следующие подстановки

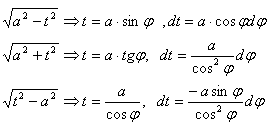
Эти подстановки позволяют избавиться от радикалов и перейти к интегралу от функции, рационально зависящей от тригонометрических функций. В свою очередь интегралы от тригонометрических функций сводятся к интегралам от рациональных дробей и вычисляются в элементарных функциях.

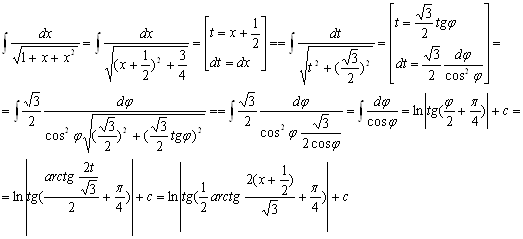
Пример 2.

< Предыдущая		Следующая >