05. Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида N>0

A) Если N Нечётное, то одну степень Sin X (либо Cos X) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.

Б) Если N чётное, то пользуемся формулами понижения степени

, .

2. Интегралы вида Где N – целое.

Необходимо использовать формулы

3. Интегралы вида

А) Пусть M и N разной чётности. Применяем подстановку , если N - нечётное либо , если M – нечётное.

Б) Если m и n чётные, то пользуемся формулами понижения степени

, .

4. Интегралы вида

Если числа M И N одинаковой чётности, то используем подстановку. Часто бывает удобным применить приём тригонометрической единицы.

5.

Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму

Пример 1.

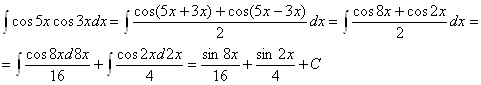
Пример 2.

Пример 3.

< Предыдущая		Следующая >