57. Контрольная работа № 6

Вариант 6.1

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

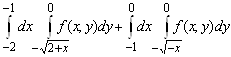3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.2

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой от точки до точки

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.3

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

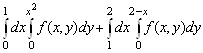3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.4

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

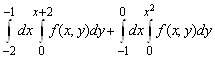3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.5

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

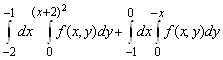3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой от точки до точки .

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.6

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

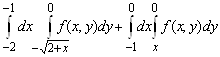3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.7

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

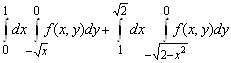3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой от точки до точки

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.8

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

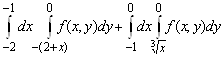3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) 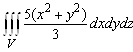, где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.9

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

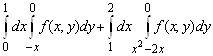3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой

7. Проверить, что поле потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

Вариант 6.10

1. Вычислить , если - внутренность треугольника с вершинами в точках .

2. Изменить порядок интегрирования

.

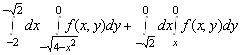3.Вычислить площадь области, заданной неравенствами

перейдя предварительно к полярным координатам.

4. Вычислить объём тела, ограниченного поверхностями

5. Вычислить интеграл (в цилиндрических или сферических координатах) , где - область, заданная неравенствами

6. Найти работу силы по перемещению точки вдоль участка кривой от точки до точки

7. Проверить, что поле Потенциально и восстановить потенциал.

8. Вычислить поток вектора Через часть поверхности , лежащую в первом октанте.

9. Вычислить поток вектора Через замкнутую поверхность

< Предыдущая		Следующая >