55. Метод вариации произвольных постоянных
Рассмотрим неоднородную систему линейных дифференциальных уравнений (5.43) ![]() или, что то же самое,
или, что то же самое,
![]() . (5.48)
. (5.48)
Пусть имеется фундаментальная система решений ![]() системы (5.44)
системы (5.44) ![]() . Тогда общее решение системы (5.44) записывается в форме
. Тогда общее решение системы (5.44) записывается в форме ![]() . Будем искать частное решение неоднородной системы уравнений (5.48) в виде
. Будем искать частное решение неоднородной системы уравнений (5.48) в виде
 (5.49)
(5.49)
Где ![]() - функции, подлежащие определению. Дифференцируя вектор-функцию (5.49), получаем
- функции, подлежащие определению. Дифференцируя вектор-функцию (5.49), получаем
 (5.50)
(5.50)
Подставляя вектор-функцию (5.49) и её производную (5.50) в систему уравнений (5.43), получаем
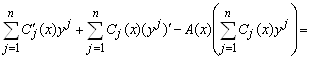
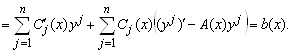 (5.51)
(5.51)
В этом соотношении слагаемое 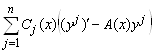 равно нулю в силу того, что
равно нулю в силу того, что ![]() - решения однородной системы уравнений (5.44)
- решения однородной системы уравнений (5.44) ![]() .
.
Поэтому правая часть в (5.51) переписывается в виде
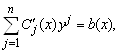 (5.52)
(5.52)
Или в координатной форме
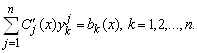 (5.52а)
(5.52а)
Так как определитель системы (5.52) есть определитель Вронского для фундаментальной системы решений ![]() однородной системы уравнений (5.44)
однородной системы уравнений (5.44) ![]() , то он отличен от нуля и поэтому система (5.52) имеет единственное решение
, то он отличен от нуля и поэтому система (5.52) имеет единственное решение ![]() которое можно найти по формулам Крамера
которое можно найти по формулам Крамера
![]() ,
,
Где ![]() определитель, полученный из определителя
определитель, полученный из определителя ![]() заменой столбца с номером
заменой столбца с номером ![]() на столбец
на столбец ![]() . Интегрируя последние равенства, окончательно получаем
. Интегрируя последние равенства, окончательно получаем
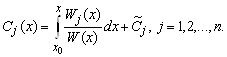
Подставляя полученные значения ![]() в (5.49), получаем общее решение
в (5.49), получаем общее решение  системы уравнений (5.43).
системы уравнений (5.43).
Пример. Для системы дифференциальных уравнений ![]() соответствующая однородная система уравнений имеет вид
соответствующая однородная система уравнений имеет вид ![]() Собственные числа её матрицы
Собственные числа её матрицы ![]() равны
равны ![]() . Собственные векторы, отвечающие этим собственным числам, равны соответственно
. Собственные векторы, отвечающие этим собственным числам, равны соответственно ![]() и
и ![]() . Тогда фундаментальная система решений состоит из функций
. Тогда фундаментальная система решений состоит из функций ![]() и
и ![]() . Решение исходной системы ищем в виде
. Решение исходной системы ищем в виде
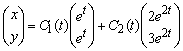 .
.
Подставляя в исходное уравнение, получаем систему
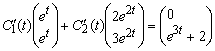 ,
,
Или в координатной форме
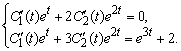
Решая эту систему, находим ![]() ,
, ![]() . Проинтегрировав, имеем
. Проинтегрировав, имеем ![]() ,
, ![]() . Таким образом, общее решение исходной системы имеет вид
. Таким образом, общее решение исходной системы имеет вид
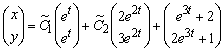 .
.
| < Предыдущая | Следующая > |
|---|