53. Системы линейных уравнений

Если в системе (5.41) все функции линейны по переменным То она называется линейной. В этом случае её можно переписать в виде

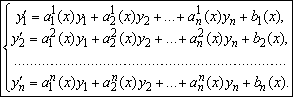(5.43)

Обозначая матрицу системы через а вектор через систему (5.43) можем переписать в матричной форме

(5.43а)

Будем, по возможности, пользоваться матричной формой записи. Если , то получаем соответствующую систему однородных уравнений

. (5.44)

Для систем линейных уравнений строится теория, полностью эквивалентная теории линейных уравнений порядка . В частности, справедлива теорема о наложении решений и её следствия. В том числе и теорема о том, что множество решений однородной системы (5.44) образует линейное подпространство в пространстве дифференцируемых вектор-функций. Сформулируем и, по возможности, докажем эти результаты.

Так же, как для векторов и систем скалярных функций, для систем вектор-функций вводятся понятия их линейной зависимости и линейной независимости.

Определение. Система вектор-функций называется линейно зависимой на отрезке , если существуют числа , не все из которых равны нулю, такие, что

Всюду на , и линейно независимой, если такого ненулевого набора не существует.

Рассмотрим совокупность вектор-функций . Определитель, составленный из их координат,

Называется определителем Вронского, или вронскианом системы вектор-функций .

Так же, как и для систем скалярных функций, определитель Вронского системы вектор-функций служит индикатором её линейной зависимости или линейной независимости.

Теорема. Если система вектор-функций линейно зависима, то её определитель Вронского равен нулю.

Доказательство аналогично соответствующему доказательству для систем векторов и систем скалярных функций, приведённому в п. 5.2.3. Предлагается сделать это самостоятельно.

Теорема. Если - линейно независимая совокупность решений однородной системы уравнений С непрерывными на Элементами матрицыИ для всех , то её определитель Вронского отличен от нуля для всех .

Доказательство аналогично соответствующему доказательству для систем скалярных функций, приведённому в п. 5.2.3. Предлагается доказать эту теорему самостоятельно.

Удостоверимся в существовании базиса в пространстве решений системы уравнений .

Теорема. Для любой однородной системы линейных дифференциальных уравнений порядка с непрерывными на Элементами матрицыИ для всех существует система линейно независимых решений этого уравнения.

Доказательство. Возьмём матрицу

(5.45)

С определителем, отличным от нуля. Тогда строки и столбцы этой матрицы линейно независимы. Найдём такие решения системы уравнений , чтобы выполнялись соотношения . По теореме существования и единственности решений такой набор решений существует. Найденная система решений линейно независима, так как её определитель Вронского в точке совпадает с определителем матрицы (5.45). Теорема доказана.

Матрицу (5.45) можно взять единичную.

Теорема (о виде общего решения однородной системы линейных дифференциальных уравнений). Если - линейно независимая совокупность решений однородной системы уравнений с непрерывными на Элементами матрицыИ для всех , то любое решение этой системы есть линейная комбинация решений , то есть

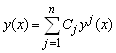
И, следовательно, - базис пространства решений системы уравнений .

Доказательство. Нам нужно доказать, что для любого набора начальных данных (5.42) можно подобрать константы так, что соответствующее решение удовлетворяет (5.42). Потребовав, чтобы решение удовлетворяло условиям (5.42), получим систему линейных алгебраических уравнений

Определитель которой и поэтому существует единственное решение этой системы.

Таким образом, нами показано, что подпространство решений однородной системы линейных дифференциальных уравнений конечномерно.

Определение. Любой базис пространства решений однородной системы линейных дифференциальных уравнений -го порядка называется фундаментальной системой решений этой системы уравнений.

Так же, как и в линейной алгебре, имеет место следующий результат.

Теорема (о виде общего решения линейной неоднородной системы дифференциальных уравнений). Общее решение линейной неоднородной системы дифференциальных уравнений с непрерывными на Элементами матрицыИ компонентами вектора , Для всех , есть сумма общего решения соответствующей однородной системы уравнений и какого либо частного решения неоднородной системы уравнений, то есть .

Доказательство. Пусть какое-нибудь фиксированное частное решение неоднородной системы линейных уравнений . Нам нужно показать, что для любого набора начальных данных можно подобрать константы так, что решение , где - фундаментальная система решений соответствующей однородной системы уравнений , удовлетворяет этому набору начальных данных. Потребовав, чтобы данное решение удовлетворяло начальным условиям, получим систему линейных алгебраических уравнений

,

Или, что то же самое,

,

Определитель которой и поэтому существует единственное решение этой системы. Теорема доказана.

< Предыдущая		Следующая >