52. Системы дифференциальных уравнений. Общая теория

Система уравнений, связывающая независимую переменную, искомые функции и некоторое количество их производных, то есть система уравнений вида

Называется системой обыкновенных дифференциальных уравнений. Если эта система разрешена относительно старших производных …, то она называется системой в канонической форме и имеет вид

Эту систему путём введения новых неизвестных функций можно привести к виду

(5.41)

В этом случае система называется системой обыкновенных дифференциальных уравнений в нормальной форме или системой обыкновенных дифференциальных уравнений в форме Коши.

Покажем, как это можно сделать для одного уравнения - го порядка. Полагаем , , . В результате можем составить систему дифференциальных уравнений

Если ввести в рассмотрение векторы , и вспомнить , что производная вектор-функции по скалярному аргументу вычисляется по формуле , то систему (5.41) можно записать в векторной форме , которая по виду совпадает с записью дифференциального уравнения первого порядка.

Для системы обыкновенных дифференциальных уравнений (5.41) можно поставить задачу Коши: найти решение Системы (5.41), удовлетворяющее начальным условиям

. (5.42)

В векторной форме условия (5.42) имеют вид .

Так же, как и для дифференциальных уравнений, для систем дифференциальных уравнений справедлива теорема существования и единственности.

Теорема. Пусть в системе уравнений (5.41)

Все функции непрерывны по совокупности переменных в области и удовлетворяют условию Липшица по переменным . Тогда найдётся окрестность точки , в которой решение системы уравнений (5.41), удовлетворяющее начальным данным (5.42), существует и единственно.

Доказательство этого результата опустим.

Если функции не зависят от , то система (5.41) называется автономной. В этом случае обычно вместо пишут и систему записывают в виде

Или в векторной форме . Если трактовать независимую переменную как время, то автономные системы отличаются тем, что их поведение не зависит от начала отсчёта переменной , а зависит от начальной точки и времени, прошедшего с начала процесса. Действительно, сделав замену переменных , получим

Более подробно с автономными системами можно ознакомиться в

В общем случае для решения систем имеются методы интегрируемых комбинаций и исключения неизвестных. Как указывалось ранее, любое уравнение порядка можно свести к системе уравнений в нормальной форме. Возможна и обратная процедура. На этой идее и основан метод исключения неизвестных. Разберём его на примерах.

Примеры

1. Для системы дифференциальных уравнений

Выражая из второго уравнения, имеем . Подставляя в первое уравнение и приводя подобные, получаем уравнение . Это линейное уравнение второго порядка с постоянными коэффициентами. Корни его характеристического уравнения равны

Поэтому . Подставляя в выражение для , получаем или, в векторной форме. .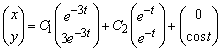

2. Найдём решение системы дифференциальных уравнений

Выражая из первого уравнения получаем . Следовательно, и, подставляя во второе уравнение, имеем Это линейное уравнение второго порядка с постоянными коэффициентами. Корни его характеристического полинома равны . Поэтому общее решение полученного уравнения есть . Подставляя в выражение для , получаем или, в векторной форме,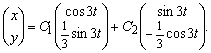

< Предыдущая		Следующая >