51. Уравнения с правой частью специального вида

Как было показано ранее, общее решение линейного неоднородного дифференциального уравнения есть сумма общего решения соответствующего однородного уравнения и какого – либо частного решения исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто. Займёмся этим вопросом.

Функцию 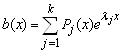, где - некоторые полиномы (многочлены), назовём квазиполиномом. По теореме о наложении решений, если - решения уравнений , то есть решение уравнения 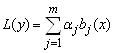. Поэтому, не умаляя общности, будем считать, что правая часть уравнения с постоянными коэффициентами имеет вид . В частности, если - комплексное число, то наиболее общей правой частью указанного типа является функция

, (5.40)

у которой И - некоторые полиномы. Справедлив следующий результат.

Теорема. Линейное дифференциальное уравнение

С постоянными коэффициентами и правой частью вида (5.40) имеет частное решение

Где - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов , - число, равное кратности корня характеристического полинома соответствующего однородного уравнения, если - корень этого полинома и , если не является корнем характеристического полинома.

Доказательство этого результата опустим.

Примеры

1. Для уравнения корнями характеристического уравнения являются кратности 1 и кратности 2. Следовательно, не является корнем характеристического уравнения. Поэтому и частное решение ищем в виде . Так как , то, подставляя в уравнение, получаем . Приравнивая коэффициенты при одинаковых степенях , получаем . Следовательно, и - частное, а - общее решения уравнения.