50. Метод вариации произвольных постоянных решения линейных неоднородных уравнений
Рассмотрим теперь линейное неоднородное уравнение (5.24)
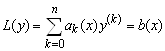 .
.
Пусть ![]() - фундаментальная система решений, а
- фундаментальная система решений, а 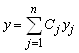 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения ![]() . Аналогично случаю уравнений первого порядка, будем искать решение уравнения (5.24) в виде
. Аналогично случаю уравнений первого порядка, будем искать решение уравнения (5.24) в виде
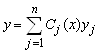 . (5.34)
. (5.34)
Убедимся в том, что решение в таком виде существует. Для этого подставим функцию в уравнение. Для подстановки этой функции в уравнение найдём её производные. Первая производная равна
 . (5.35)
. (5.35)
При вычислении второй производной в правой части (5.35) появится четыре слагаемых, при вычислении третьей производной - восемь слагаемых и так далее. Так как при подстановке решения (5.34) в уравнение (5.24) получается одно соотношение на ![]() неизвестных функций, то остальные
неизвестных функций, то остальные ![]() находятся в нашей власти. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (5.35) полагают равным нулю. С учётом этого, вторая производная равна
находятся в нашей власти. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (5.35) полагают равным нулю. С учётом этого, вторая производная равна
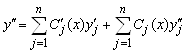 . (5.36)
. (5.36)
По тем же, что и раньше, соображениям, в (5.36) также полагаем первое слагаемое равным нулю. Наконец, ![]() - я производная равна
- я производная равна
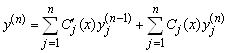 . (5.37)
. (5.37)
Подставляя полученные значения производных в исходное уравнение, имеем
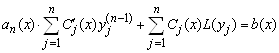 . (5.38)
. (5.38)
Второе слагаемое в (5.38) равно нулю, так как функции ![]() являются решениями соответствующего однородного уравнения
являются решениями соответствующего однородного уравнения ![]() . Объединяя (5.38) с полученными при вычислении производных условиями, получаем систему алгебраических уравнений для нахождения функций
. Объединяя (5.38) с полученными при вычислении производных условиями, получаем систему алгебраических уравнений для нахождения функций ![]()
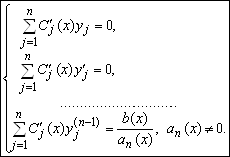 (5.39)
(5.39)
Определитель этой системы есть определитель Вронского фундаментальной системы решений ![]() соответствующего однородного уравнения
соответствующего однородного уравнения ![]() и поэтому не равен нулю. Следовательно, существует единственное решение системы (5.39). Найдя его, получим функции
и поэтому не равен нулю. Следовательно, существует единственное решение системы (5.39). Найдя его, получим функции ![]() а, следовательно, и
а, следовательно, и ![]() . Подставляя эти значения в (5.34), получаем решение линейного неоднородного уравнения.
. Подставляя эти значения в (5.34), получаем решение линейного неоднородного уравнения.
Для ![]() , то есть для уравнения второго порядка, система уравнений (5.39) приобретает вид
, то есть для уравнения второго порядка, система уравнений (5.39) приобретает вид
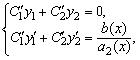
А для ![]() система (5.39) записывается в виде
система (5.39) записывается в виде
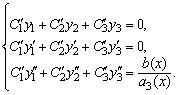
Изложенный метод называется методом вариации произвольной постоянной или методом Лагранжа.
Примеры
1. Найдём общее решение уравнения ![]() . Рассмотрим соответствующее однородное уравнение
. Рассмотрим соответствующее однородное уравнение ![]() . Корни его характеристического уравнения
. Корни его характеристического уравнения ![]() равны
равны ![]() и
и ![]() . Поэтому фундаментальная система решений однородного уравнения состоит из функций
. Поэтому фундаментальная система решений однородного уравнения состоит из функций ![]() и
и ![]() . Решение неоднородного уравнения ищем в виде
. Решение неоднородного уравнения ищем в виде ![]() . Для нахождения производных
. Для нахождения производных ![]() составляем систему уравнений (5.39)
составляем систему уравнений (5.39)
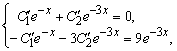
Решая которую, находим ![]() ,
, ![]() . Интегрируя полученные функции, имеем
. Интегрируя полученные функции, имеем ![]() ,
, ![]() . Подставляя
. Подставляя ![]() и
и ![]() в выражение для
в выражение для ![]() , окончательно находим
, окончательно находим ![]() .
.
2. Найдём общее решение уравнения ![]() . Пример отличается от предыдущего лишь правой частью. Поэтому изменяется лишь система уравнений для нахождения производных
. Пример отличается от предыдущего лишь правой частью. Поэтому изменяется лишь система уравнений для нахождения производных ![]() , приобретающая вид
, приобретающая вид
![]()
Решая эту систему, находим ![]() ,
, ![]() . Отсюда, интегрируя, имеем
. Отсюда, интегрируя, имеем ![]() ,
, ![]() . Подставляя
. Подставляя ![]() и
и ![]() в выражение для
в выражение для ![]() , окончательно находим
, окончательно находим ![]() .
.
3. Найдём общее решение уравнения ![]() . Корни характеристического полинома
. Корни характеристического полинома ![]() соответствующего однородного уравнения равны
соответствующего однородного уравнения равны ![]() ,
, ![]() ,
, ![]() . Поэтому фундаментальная система решений однородного уравнения состоит из функций
. Поэтому фундаментальная система решений однородного уравнения состоит из функций ![]() ,
, ![]() ,
, ![]() Решение неоднородного уравнения ищем в виде
Решение неоднородного уравнения ищем в виде ![]() . Для нахождения производных
. Для нахождения производных ![]() составляем систему уравнений (5.39)
составляем систему уравнений (5.39)
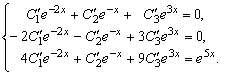
Решая эту систему, находим ![]() ,
, ![]() ,
, ![]() . Интегрируя полученные функции, имеем
. Интегрируя полученные функции, имеем ![]() ,
, ![]() ,
, ![]() . Подставляя
. Подставляя ![]() ,
, ![]() ,
, ![]() в выражение для
в выражение для ![]() окончательно находим
окончательно находим ![]() .
.
| < Предыдущая | Следующая > |
|---|