49. Линейные дифференциальные уравнения с постоянными коэффициентами

Поиск фундаментальной системы решений в общем случае является достаточно трудной задачей. Тем не менее, есть класс уравнений, для которого эта задача достаточно легко решается. К изучению этого класса мы и приступаем.

Линейное дифференциальное уравнение (5.24) назовём уравнением с постоянными коэффициентами, если в этом уравнении коэффициенты постоянны, то есть . Тогда соответствующее однородное уравнение Будет иметь вид

(5.27)

Решение уравнения (5.27) будем искать в виде . Тогда , ,…, . Подставляя в (5.27), получаем

.

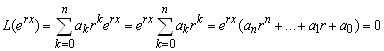Так как Нигде в нуль не обращается, то

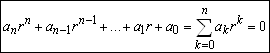. (5.28)

Уравнение (5.28) называется характеристическим уравнением линейного однородного дифференциального уравнения с постоянными коэффициентами.

Таким образом, нами доказана следующая теорема.

Теорема. Функция является решением линейного однородного дифференциального уравнения с постоянными коэффициентами (5.27) тогда и только тогда, когда есть корень характеристического уравнения (5.28).

Возможны нижеследующие случаи.

1. Все корни характеристического многочлена вещественны и различны. Обозначим их . Тогда получим различных решений

, ,…, (5.29)

Уравнения (5.27). Докажем, что полученная система решений линейно независима. Рассмотрим её определитель Вронского

.

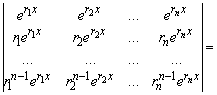
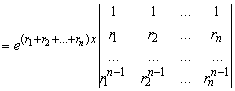Множитель в правой части нигде в нуль не обращается. Поэтому осталось показать, что второй сомножитель (определитель) не равен нулю. Допустим, что

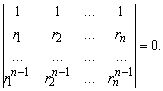
Тогда строки этого определителя линейно зависимы, т. е. существуют числа такие, что

, , … , .

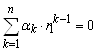Таким образом, мы получили, что есть различных корней полинома - й степени, что невозможно. Следовательно, определитель в правой части не равен нулю и система функций (5.29) образует фундаментальную систему решений уравнения (5.27) в случае, когда корни характеристического уравнения различны.

Пример. Для уравнения корни характеристического уравнения равны , . Следовательно, фундаментальную систему решений составляют функции ,, а общее решение записывается в виде .

2. Среди действительных корней характеристического уравнения есть кратные. Предположим, что имеет кратность , а все остальные различны. Рассмотрим вначале случай . Тогда характеристическое уравнение имеет вид

,

Так как в противном случае не являлось бы корнем кратности . Следовательно, дифференциальное уравнение имеет вид

,

То есть не содержит производных порядка ниже . Этому уравнению удовлетворяют все функции, у которых производные порядка и выше равны нулю. В частности, таковыми являются все полиномы степени не выше , например,

. (5.30)

Покажем, что данная система линейно независима. Составив определитель Вронского этой системы функций, получим

.

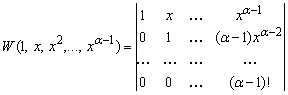Это определитель треугольного вида с отличными от нуля элементами, стоящими на главной диагонали. Поэтому он отличен от нуля, что и доказывает линейную независимость системы функций (5.30). Заметим, что в одном из примеров предыдущего параграфа мы доказывали линейную независимость системы функций (5.30) другим способом. Пусть теперь корнем характеристического уравнения кратности является число . Произведём в уравнении (5.27) замену . Тогда

И так далее. Подставляя полученные значения производных в исходное уравнение, снова получим линейное однородное уравнение с постоянными коэффициентами

(5.31)

С характеристическим уравнением

. (5.32)

Отметим, что если - корень характеристического уравнения (5.32), то - решение уравнения (5.31), а является решением уравнения (5.27). Тогда - корень характеристического уравнения (5.28). С другой стороны, уравнение (5.27) может быть получено из уравнения (5.31) обратной заменой И поэтому каждому корню характеристического уравнения (5.28) соответствует корень характеристического уравнения (5.32). Таким образом, установлено взаимно однозначное соответствие между корнями характеристических уравнений (5.28) и (5.32), причём различным корням одного уравнения соответствуют различные корни другого. Так как - корень кратности уравнения (5.28), то уравнение (5.32) имеет корнем кратности . По доказанному ранее, уравнение (5.31) имеет линейно независимых решений

,

Которым соответствует линейно независимых решений

(5.33)

Уравнения (5.27). Присоединяя полученную систему решений (5.33) к решениям, соответствующим остальным корням характеристического уравнения, получим фундаментальную систему решений для линейного однородного дифференциального уравнения с постоянными коэффициентами в случае наличия действительных кратных корней.

Примеры

1. Для уравнения характеристическое уравнение имеет корни кратности 1 и кратности 2, так как . Поэтому фундаментальной системой решений исходного уравнения является система функций , а общее решение имеет вид

2. Для уравнения характеристическое уравнение имеет корни кратности 3 и кратности 2, так как . Поэтому фундаментальной системой решений исходного уравнения является система функций , а общее решение имеет вид .

3. Среди корней характеристического уравнения есть комплексные корни. Можно рассматривать комплексные решения, но для уравнений с действительными коэффициентами это не очень удобно. Найдём действительные решения, соответствующие комплексным корням. Так как мы рассматриваем уравнение с действительными коэффициентами, то для каждого комплексного корня кратности характеристического уравнения комплексно сопряжённое ему число также является корнем кратности этого уравнения. Соответствующими этим корням парами решений являются функции и , . Вместо этих решений рассмотрим их линейные комбинации

,

, которые также являются решениями уравнения . Так как преобразование, осуществляющее переход от к ,, невырожденное (с отличным от нуля определителем), то оно переводит линейно независимую систему решений в линейно независимую.

Примеры

1. Для уравнения корни характеристического уравнения равны и фундаментальная система решений состоит из функций а общее решение имеет вид

2. Для уравнения корни характеристического уравнения равны , и фундаментальная система решений состоит из функций а общее решение имеет вид

3. Для уравнения характеристическое уравнение имеет корни кратности 2, так как . Поэтому фундаментальной системой решений исходного уравнения является система функций , а общее решение имеет вид

< Предыдущая		Следующая >