44. Уравнения в полных дифференциалах

Рассмотрим дифференциальное уравнение

. (5.15)

Если существует функция такая, что

,

То уравнение (5.15) называется уравнением в полных дифференциалах.

В этом случае его можно записать в виде . Тогда . Если разрешить последнее соотношение относительно , то получим общее решение уравнения (5.15).

Примеры

1. Дифференциальное уравнение является уравнением в полных дифференциалах, так как . Поэтому Есть общее решение этого уравнения.

2. Аналогично для уравнения выражение есть общее решение, так как левая часть этого уравнения является дифференциалом функции

Как видим, уравнения в полных дифференциалах легко решаются, если знать функцию, дифференциалом которой является левая часть уравнения.

Вспоминая определение потенциальности поля , получаем справедливость следующей теоремы.

Теорема. Уравнение (5.15) есть уравнение в полных дифференциалах тогда и только тогда, когда поле потенциально, или, что то же самое, криволинейный интеграл не зависит от пути интегрирования.

Следствие. Если существуют непрерывные производные то уравнение (5.15) есть уравнение в полных дифференциалах тогда и только тогда, когда

Следствие даёт возможность выяснить, является ли уравнение уравнением в полных дифференциалах или нет. Теорема позволяет найти решение уравнения в случае положительного ответа на предыдущий вопрос.

Примеры

1. Найти общее решение уравнения . Так как , то данное уравнение является уравнением в полных дифференциалах. Поэтому, восстанавливая потенциал, получаем

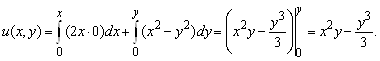Тогда общий интеграл (общее решение) имеет вид

2. Уравнение также является уравнением в полных дифференциалах, так как

Поэтому, восстанавливая потенциал, имеем

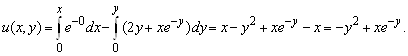
Следовательно, общий интеграл (общее решение) уравнения равен

Взяв дифференциал некоторой функции двух переменных и приравняв его к нулю, получим уравнение в полных дифференциалах. Сократив на общий множитель (если он есть), мы, скорее всего, получим уравнение, не являющееся уравнением в полных дифференциалах. Поэтому возникает обратная задача: нельзя ли подобрать функцию так, чтобы, умножив на неё уравнение в дифференциальной форме, получить уравнение в полных дифференциалах. Эта задача носит название задачи о нахождении интегрирующего множителя. Оказывается, что найти интегрирующий множитель можно, но соотношения, позволяющие сделать это, часто оказываются более сложными, чем само уравнение.

Задание 5.4.

Найдите решения дифференциальных уравнений:

1. ; 2..

Ответы: 1. ; 2. .

< Предыдущая		Следующая >