42. Линейные уравнения первого порядка

Уравнение первого порядка вида

(5.9)

Называется линейным дифференциальным уравнением. Если то уравнение (5.9) называется линейным однородным, в противном случае – линейным неоднородным. Для линейного дифференциального уравнения теорема существования и единственности имеет более конкретный вид.

Теорема. Пусть , , непрерывны на отрезке , для . Тогда для любой точки , , существует единственное решение уравнения (5.9), удовлетворяющее условию и определенное на всем интервале .

Рассмотрим однородное линейное дифференциальное уравнение

. (5.10)

Разделяя переменные, получаем , или, интегрируя обе части, 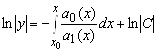. Последнее соотношение, с учетом обозначения , записывается в форме

(5.11)

Заметим, что выбор точки влияет лишь на вид конкретной первообразной функции .

Будем искать решение линейного неоднородного дифференциального уравнения (5.9) Методом Лагранжа или, что то же самое, Методом вариации произвольной постоянной.

Суть метода заключается в том, что мы пытаемся найти решение уравнения (5.9) в виде (5.11), в котором вместо константы подставлена функция то есть в виде

(5.12)

Подставив решение (5.12) в (5.9), получаем . Интегрируя последнее, имеем

Где - некоторая новая константа. Подставляя полученное выражение для в (5.12), окончательно получаем общее решение исходного линейного уравнения

.

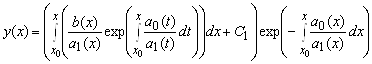Примеры.

1. Решить уравнение . Рассмотрим соответствующее однородное уравнение . Решая его, получаем (при ) . Ищем теперь решение исходного уравнения в виде . Подставляя и В исходное уравнение, имеем откуда и, подставляя полученное выражение в , получаем общее решение исходного уравнения .

2. Решить уравнение . Рассмотрим соответствующее однородное уравнение . Решая его, получаем , , . Ищем теперь решение исходного уравнения в виде . Подставляя и В исходное уравнение, имеем Откуда и - общее решение исходного уравнения.

3. Решить уравнение . Рассмотрим соответствующее однородное уравнение . Решая его, получаем , , . Ищем теперь решение исходного уравнения в виде . Подставляя и в исходное уравнение, имеем откуда и - общее решение исходного уравнения.

4. Решить уравнение . Вспоминая, что переменные и в дифференциальном уравнении равноправны и переписывая его в виде , или, что то же самое, в форме , получим, что данное уравнение является линейным относительно и . Рассмотрим соответствующее однородное уравнение . Решая его, получаем , , . Ищем теперь решение уравнения в виде . Подставляя и В него, имеем откуда и - общее решение исходного уравнения.

< Предыдущая		Следующая >