36. Вычисление и свойства
Пусть кривая задана параметрически 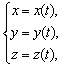 или, что то же самое, в векторной форме,
или, что то же самое, в векторной форме,
 .
.
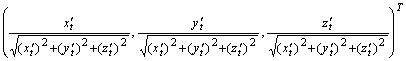
Тогда вектор касательной приобретает вид ![]() , а единичный вектор касательной
, а единичный вектор касательной ![]() равен
равен
Так как ![]() , то
, то
![]()
И для криволинейного интеграла второго рода имеем

В случае плоской кривой ![]()
![]() Получим
Получим
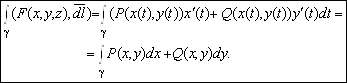
Если плоская кривая задана явно уравнением ![]() , то её можно считать заданной параметрически
, то её можно считать заданной параметрически ![]() взяв в качестве параметра
взяв в качестве параметра ![]() Тогда последняя формула приобретает вид
Тогда последняя формула приобретает вид
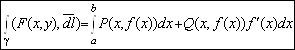 .
.
Заметим, что все формулы для вычисления криволинейного интеграла второго рода получены при соглашении, что направлением обхода кривой считается направление, задаваемое вектором касательной ![]() , если кривая задана параметрически или векторно, и вектором касательной
, если кривая задана параметрически или векторно, и вектором касательной ![]() , если кривая задана явно. Если по каким-либо соображениям обходить кривую необходимо в обратном направлении, то все знаки в формулах нужно поменять на противоположные.
, если кривая задана явно. Если по каким-либо соображениям обходить кривую необходимо в обратном направлении, то все знаки в формулах нужно поменять на противоположные.
Если поверхность задана параметрически 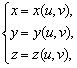 или, что то же самое, в векторной форме
или, что то же самое, в векторной форме
![]()
![]()
То при задании стороны поверхности с помощью вектора нормали ![]() единичный вектор нормали равен
единичный вектор нормали равен ![]() и, так как
и, так как ![]() , то
, то ![]()

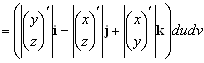 , где
, где  ,
,  ,
, 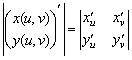 - якобианы (определители матриц Якоби, или, что то же самое, матриц производных)
- якобианы (определители матриц Якоби, или, что то же самое, матриц производных)![]() вектор-функций
вектор-функций ![]()
![]() соответственно. Тогда для вычисления поверхностного интеграла второго рода получаем формулу
соответственно. Тогда для вычисления поверхностного интеграла второго рода получаем формулу
![]()

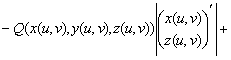

Пусть поверхность ![]() задана явно уравнением
задана явно уравнением![]() ,
, ![]() . Тогда, если в качестве параметров взять
. Тогда, если в качестве параметров взять ![]() , её можно считать заданной в векторной форме
, её можно считать заданной в векторной форме ![]()
![]() , или, что то же самое, параметрически
, или, что то же самое, параметрически 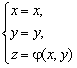 . Тогда
. Тогда ![]() ,
, ![]() ,
, ![]() и поверхностный интеграл второго рода вычисляется по формуле
и поверхностный интеграл второго рода вычисляется по формуле
![]() ,
,
В которой ![]() , а
, а ![]() есть проекция поверхности
есть проекция поверхности ![]() на плоскость
на плоскость ![]() . Получить аналогичные формулы в случае, когда поверхность задана явно одним из уравнений
. Получить аналогичные формулы в случае, когда поверхность задана явно одним из уравнений ![]() или
или ![]() , предлагается читателю.
, предлагается читателю.
Напомним, что мы получили формулы для вычисления поверхностного интеграла второго рода при ориентации поверхности с помощью вектора нормали ![]() . При необходимости выбора другой стороны поверхности все знаки в формулах поменяются на противоположные.
. При необходимости выбора другой стороны поверхности все знаки в формулах поменяются на противоположные.
Рассмотрим теперь более подробно интегральную сумму, используемую в определении поверхностного интеграла второго рода. Для удобства записи введём обозначения ![]() . Имеем
. Имеем

Где ![]()
![]() - направляющие косинусы (координаты) единичного вектора нормали
- направляющие косинусы (координаты) единичного вектора нормали ![]() ,
, ![]() - площадь элементарного участка
- площадь элементарного участка ![]() поверхности
поверхности![]() . Рассмотрим проекцию элементарного участка
. Рассмотрим проекцию элементарного участка ![]() поверхности на одну из координатных плоскостей, например, на плоскость
поверхности на одну из координатных плоскостей, например, на плоскость ![]() . Площадь
. Площадь ![]() Этой проекции равна
Этой проекции равна ![]() , где
, где ![]() - угол между плоскостью
- угол между плоскостью ![]() и касательной плоскостью к поверхности в точке
и касательной плоскостью к поверхности в точке ![]() . Знак плюс берётся, если этот угол острый, и минус, если этот угол тупой. По определению угла между плоскостями, этот угол совпадает с углом между нормальными векторами этих плоскостей, то есть с углом
. Знак плюс берётся, если этот угол острый, и минус, если этот угол тупой. По определению угла между плоскостями, этот угол совпадает с углом между нормальными векторами этих плоскостей, то есть с углом ![]() между векторами
между векторами ![]() и
и ![]() . Таким образом,
. Таким образом, ![]() . Обозначив через
. Обозначив через ![]() площадь проекции
площадь проекции ![]() на плоскость
на плоскость ![]() , а через
, а через ![]() площадь проекции
площадь проекции ![]() на плоскость
на плоскость ![]() , можно аналогично показать, что
, можно аналогично показать, что ![]() . Поэтому
. Поэтому ![]() . Последнее даёт право записать поверхностный интеграл второго рода в стандартном виде
. Последнее даёт право записать поверхностный интеграл второго рода в стандартном виде
![]()
![]() ,
,
А если поверхность ![]() может быть задана одновременно уравнениями
может быть задана одновременно уравнениями ![]() то вычислять поверхностный интеграл второго рода по формуле
то вычислять поверхностный интеграл второго рода по формуле
![]()
![]()
![]()
Где ![]() - проекции поверхности
- проекции поверхности ![]() на координатные плоскости
на координатные плоскости ![]() соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–”, если этот угол тупой.
соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–”, если этот угол тупой.
Заметим, что для криволинейного и поверхностного интегралов имеют место общие для всех интегралов свойства. Отметим некоторые из них в формулировках, отражающих специфику этих интегралов.
Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее
![]() .
.
Доказательство опустим.
Замечание. Если в качестве ориентированной кривой взять отрезок ![]() оси
оси ![]() с направлением обхода от
с направлением обхода от ![]() к
к ![]() , то определённый интеграл
, то определённый интеграл ![]() можно рассматривать как криволинейный интеграл второго рода по этой кривой, а теорему 1 считать обобщением свойства 1 определённого интеграла на случай ориентированного многообразия..
можно рассматривать как криволинейный интеграл второго рода по этой кривой, а теорему 1 считать обобщением свойства 1 определённого интеграла на случай ориентированного многообразия..
Теорема 2. Пусть ![]() и размерность пересечения
и размерность пересечения ![]() Тогда
Тогда
![]()
Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу ![]() с
с ![]() , получаем требуемое.
, получаем требуемое.
Теорема 3 (о среднем для криволинейного интеграла). Если функция ![]() непрерывна на гладкой кривой
непрерывна на гладкой кривой ![]() , то существует точка
, то существует точка ![]() на кривой
на кривой ![]() такая, что для криволинейного интеграла второго рода выполнено соотношение
такая, что для криволинейного интеграла второго рода выполнено соотношение
![]() ,
,
Где ![]() - длина кривой
- длина кривой ![]() .
.
Доказательство опустим.
Теорема 4 (о среднем для поверхностного интеграла). Если функция ![]() непрерывна на гладкой поверхности
непрерывна на гладкой поверхности ![]() , то существует точка
, то существует точка ![]() поверхности
поверхности ![]() , такая, что для поверхностного интеграла второго рода выполнено равенство
, такая, что для поверхностного интеграла второго рода выполнено равенство
![]() ,
,
Где ![]() - площадь поверхности
- площадь поверхности ![]() .
.
Доказательство опустим.
Примеры
1. Вычислить ![]() вдоль кривой
вдоль кривой ![]()
Если![]()
Имеем
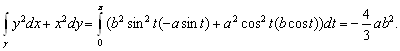
2. Найти работу по перемещению материальной точки под действием силы ![]() вдоль одного витка винтовой линии
вдоль одного витка винтовой линии ![]() .
.
Работа по перемещению материальной точки равна криволинейному интегралу второго рода ![]() . Так как кривая задана параметрически и
. Так как кривая задана параметрически и ![]() , то
, то

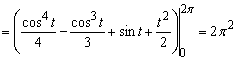 .
.
3. Вычислить поток вектора ![]() через часть плоскости
через часть плоскости ![]() лежащую в первом октанте.
лежащую в первом октанте.
Поток вектора через поверхность равен поверхностному интегралу второго рода ![]() . Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
. Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда
![]()
![]()
![]() ,
,
Где ![]() - проекции поверхности
- проекции поверхности ![]() на координатные плоскости
на координатные плоскости ![]() соответственно. Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Посчитаем первый интеграл. Имеем
соответственно. Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Посчитаем первый интеграл. Имеем 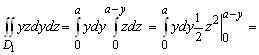
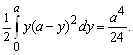 Третий интеграл считается аналогично и также равен
Третий интеграл считается аналогично и также равен ![]()
Для второго интеграла имеем ![]()
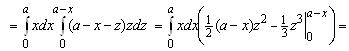
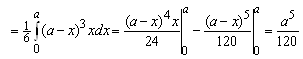 .
.
Поэтому поток вектора через поверхность равен ![]() .
.
4. Вычислить поток вектора ![]() через верхнюю половину сферы радиуса
через верхнюю половину сферы радиуса ![]() в сторону внешней нормали.
в сторону внешней нормали.
Параметрическое уравнение верхней половины сферы радиуса ![]() можно написать в виде
можно написать в виде ![]() ,
, ![]() ,
, ![]() , где
, где ![]() , или, что то же самое, в векторной форме
, или, что то же самое, в векторной форме ![]() . Тогда
. Тогда
![]() ,
,![]()
Поэтому

![]() .
.
Этот вектор образует с осью ![]() Тупой угол, поэтому в качестве вектора нормали берём вектор
Тупой угол, поэтому в качестве вектора нормали берём вектор ![]() . Подставляя выражения
. Подставляя выражения ![]() в функцию
в функцию ![]() и вычисляя скалярное произведение
и вычисляя скалярное произведение ![]() , получаем
, получаем ![]() .
.
Поэтому поток вектора через поверхность равен
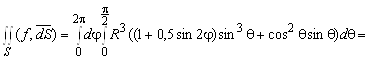
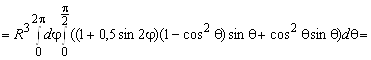
 .
.
Задание 4.2
1. Вычислить ![]() а) вдоль кривой
а) вдоль кривой ![]() от точки
от точки ![]() до точки
до точки ![]() ; б) вдоль кривой
; б) вдоль кривой ![]() ,
, ![]() ; в) вдоль прямой, соединяющей точки
; в) вдоль прямой, соединяющей точки ![]() .
.
2. Найти работу по перемещению материальной точки под действием силы ![]() а) вдоль кривой
а) вдоль кривой ![]() ,
, ![]() ; б) вдоль прямой, соединяющей точки
; б) вдоль прямой, соединяющей точки ![]() .
.
3. Вычислить поток вектора ![]() через часть поверхности
через часть поверхности ![]() , заключённой между координатными плоскостями.
, заключённой между координатными плоскостями.
4. Вычислить поток вектора ![]() через нижнюю половину сферы радиуса
через нижнюю половину сферы радиуса ![]() .
.
Ответы: 1. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; 2. а)
; 2. а) ![]() ; б)
; б)![]() ; 3. 84; 4.
; 3. 84; 4. ![]() .
.
| < Предыдущая | Следующая > |
|---|