33. Криволинейные и поверхностные интегралы первого рода

Кривую или поверхность будем называть многообразием.

Определение. Пусть задано непрерывное кусочно-гладкое многообразие и на – функция . Разобьем на части многообразиями меньшей размерности (кривую – точками, поверхность – кривыми) и внутри каждого полученного элементарного многообразия выберем по точке . Посчитаем значения функции в этих точках, умножим эти значения на меру данного элементарного многообразия (длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных Сумм, если он существует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если – кривая, и поверхностным, если – поверхность) первого рода и обозначается в общем случае, в случаях криволинейного и поверхностного интегралов соответственно.

Если кривая задана параметрически 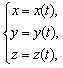или, что тo же самое, в векторной форме

, то и поэтому криволинейный интеграл первого рода вычисляется по формуле

.

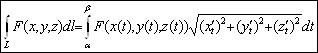В случае плоской кривой

()

Эта формула приобретает вид

Пусть плоская кривая задана явно уравнением Всякую такую кривую можно считать заданной параметрически взяв в качестве параметра Тогда последняя формула приобретает вид

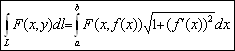
Для поверхности, заданной параметрически 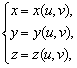или, что то же самое, в векторной форме

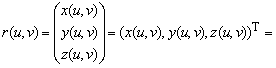
И поэтому поверхностный интеграл первого рода вычисляется по формуле

Если поверхность задана явно уравнением то , и последняя формула приобретает вид

,

Где - проекция поверхности на плоскость .

Теорема. Величина криволинейного (поверхностного) интеграла первого рода не изменяется при изменении ориентации кривой (поверхности), то есть

Доказательство. Докажем теорему для криволинейного интеграла и кривой, заданной параметрически. Введем новый параметр T По формуле Тогда

.

Заметим, что когда движется от к , то движется от к и наоборот. При этом и кривая обходится в противоположном направлении. Поэтому

Где ,

- норма(длина) векторов и соответственно. Теорема доказана.

Примеры

1. Вычислить , где а) g - парабола , б) g - прямая, соединяющая точки (0, 0) и (1, 1).

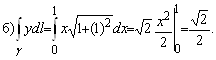
2. Вычислить вдоль кривой

Если

Имеем

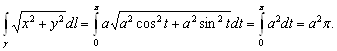
3. Вычислить поверхностный интеграл если поверхность есть часть плоскости лежащая в первом октанте.

Эта поверхность задаётся явно уравнением . Тогда Проекция поверхности на плоскость есть треугольник , ограниченный кривыми Поэтому

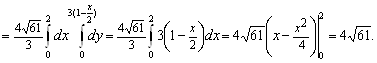
Задание 4.1

1. Вычислить а) вдоль кривой ; б) вдоль прямой, соединяющей точки .

2. Вычислить вдоль прямой, соединяющей точки .

3. Вычислить вдоль кривой , ;

4. . Вычислить поверхностный интеграл если поверхность есть часть плоскости лежащая в части пространства .

Ответы:

1. а) ; б) ; 2. ; 3. ; 4. .

< Предыдущая		Следующая >