32. Поверхности в пространстве

Рассмотрим вектор-функцию двух аргументов

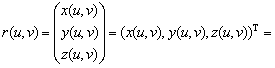
Где - векторы декартова базиса. Если функции непрерывны и начала всех векторов поместить в начало координат, то их концы опишут в некоторую поверхность, называемую годографом вектор-функции , а вектор-функцию называют векторным представлением этой поверхности. Поверхность будем обозначать одной из букв

Поверхность назовем гладкой, если существуют непрерывные производные и Непрерывную поверхность назовём кусочно-гладкой, если её можно разбить на конечное число поверхностей, каждая из которых гладкая.

Фиксируя , получаем кривую , и вектор направлен по касательной к этой кривой. Аналогично направлен по касательной к кривой при фиксированном Поэтому и лежат в касательной плоскости к (если она существует). Тогда - вектор нормали к поверхности . Фиксируя направление нормали фиксируем ориентацию поверхности.

Назовём поверхность двухсторонней, если нельзя перейти по поверхности непрерывным образом из точки в ту же точку, но с противоположным направлением нормали. В противном случае поверхность назовем односторонней. Классическим примером односторонней поверхности является лист Мёбиуса. Модель листа Мёбиуса можно получить, если склеить полоску бумаги, предварительно повернув одну из коротких сторон на . Мы будем иметь дело с двухсторонними поверхностями.

< Предыдущая		Следующая >