28. Приложения кратных интегралов. Вычисление площадей плоских фигур

Из определения двойного интеграла следует, что площадь плоской области выражается по формуле . Если область есть криволинейная трапеция, ограниченная линиями и для , то

- формула площади области , полученная нами в п. 2.6.1.

Пример. Найти площадь фигуры, ограниченной линиями Имеем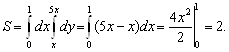

< Предыдущая		Следующая >