27. Примеры замены переменных в интегралах
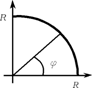 1. В интеграле
1. В интеграле 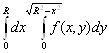 перейдём к полярным координатам. Так как область интегрирования есть четверть круга радиуса
перейдём к полярным координатам. Так как область интегрирования есть четверть круга радиуса ![]() , лежащая в первом квадранте, то
, лежащая в первом квадранте, то 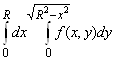 =
= .
.
 2. Пусть область
2. Пусть область ![]() - внутренность треугольника с вершинами
- внутренность треугольника с вершинами ![]() ,
, ![]() ,
, ![]() . В интеграле
. В интеграле ![]() перейти к полярным координатам и расставить пределы интегрирования в нём.
перейти к полярным координатам и расставить пределы интегрирования в нём.
Уравнения прямых ![]() ,
, ![]() и
и ![]() -
- ![]() ,
, ![]() и
и ![]() соответственно. Поэтому угол
соответственно. Поэтому угол ![]() между радиус-вектором точки, принадлежащей треугольнику
между радиус-вектором точки, принадлежащей треугольнику ![]() , и осью
, и осью ![]() меняется в пределах
меняется в пределах ![]() . Уравнение прямой
. Уравнение прямой ![]() в полярных координатах переписывается в виде
в полярных координатах переписывается в виде ![]() , или, что то же самое,
, или, что то же самое, ![]() . Поэтому
. Поэтому
 .
.
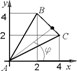 3. Пусть область
3. Пусть область ![]() - внутренность треугольника с вершинами
- внутренность треугольника с вершинами ![]() ,
, ![]() ,
, ![]() . В интеграле
. В интеграле ![]() перейти к полярным координатам и расставить пределы интегрирования в нём.
перейти к полярным координатам и расставить пределы интегрирования в нём.
Уравнения прямых ![]() ,
, ![]() и
и ![]() -
- ![]() ,
, ![]() и
и ![]() соответственно. Поэтому угол
соответственно. Поэтому угол ![]() между радиус-вектором точки, принадлежащей треугольнику
между радиус-вектором точки, принадлежащей треугольнику ![]() , и осью
, и осью ![]() меняется в пределах
меняется в пределах ![]() . Уравнение прямой
. Уравнение прямой ![]() в полярных координатах переписывается в виде
в полярных координатах переписывается в виде ![]() , или, что то же самое,
, или, что то же самое, ![]() . Поэтому
. Поэтому
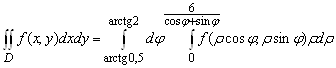 .
.
4. Пусть область ![]() - внутренность треугольника с вершинами
- внутренность треугольника с вершинами ![]() ,
, ![]() ,
, ![]() . В интеграле
. В интеграле ![]() перейти к полярным координатам и расставить пределы интегрирования в нём.
перейти к полярным координатам и расставить пределы интегрирования в нём.
Уравнения прямых ![]() ,
, ![]() и
и ![]() есть
есть ![]() ,
, ![]() и
и ![]() соответственно. Уравнение прямой
соответственно. Уравнение прямой ![]() в полярных координатах имеет вид
в полярных координатах имеет вид ![]() , или, выражая
, или, выражая ![]() через
через ![]() ,
, ![]() , уравнение прямой
, уравнение прямой ![]() имеет вид
имеет вид ![]() , или
, или ![]() , а уравнение прямой
, а уравнение прямой ![]() переписывается в виде
переписывается в виде ![]() , или, что то же самое,
, или, что то же самое, ![]() . С учётом того, что при изменении угла
. С учётом того, что при изменении угла ![]() в пределах
в пределах ![]() и
и ![]() длина радиус-вектора точки, принадлежащей треугольнику
длина радиус-вектора точки, принадлежащей треугольнику ![]() , меняется в разных пределах, имеем
, меняется в разных пределах, имеем ![]()
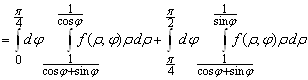 .
.
 5. Пусть область
5. Пусть область ![]() - внутренность круга с центром в точке
- внутренность круга с центром в точке ![]() и радиуса 1. В интеграле
и радиуса 1. В интеграле ![]() перейти к полярным координатам и расставить пределы интегрирования в нём.
перейти к полярным координатам и расставить пределы интегрирования в нём.
Уравнение данной окружности в декартовых координатах записывается в виде ![]() , или, после преобразований,
, или, после преобразований, ![]() . Переходя к полярным координатам, получаем для этой окружности уравнение
. Переходя к полярным координатам, получаем для этой окружности уравнение ![]() . Поэтому
. Поэтому
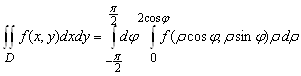 .
.
 6. Пусть область
6. Пусть область ![]() задана неравенствами
задана неравенствами ![]() ,
, ![]() . Перейти к полярным координатам и расставить пределы интегрирования в интеграле
. Перейти к полярным координатам и расставить пределы интегрирования в интеграле ![]() . Уравнение окружности
. Уравнение окружности ![]() в полярных координатах имеет вид
в полярных координатах имеет вид ![]() , а окружности
, а окружности ![]() имеет вид
имеет вид ![]() . Поэтому
. Поэтому
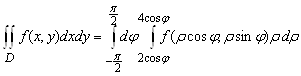 .
.
Для сферической системы координат матрица Якоби
![]() равна
равна
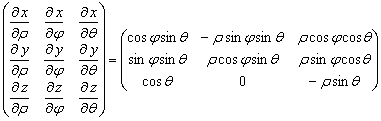 .
.
Определитель этой матрицы ![]() равен
равен ![]() , поэтому модуль Якобиана
, поэтому модуль Якобиана ![]() равен
равен ![]() , и формула перехода к сферическим координатам в тройном интеграле приобретает вид
, и формула перехода к сферическим координатам в тройном интеграле приобретает вид
![]()
![]() .
.
Для цилиндрической системы координат матрица Якоби ![]() равна
равна
 .
.
Определитель этой матрицы ![]() равен
равен ![]() , поэтому модуль Якобиана
, поэтому модуль Якобиана ![]() также равен
также равен ![]() и формула перехода к цилиндрическим координатам в тройном интеграле приобретает вид
и формула перехода к цилиндрическим координатам в тройном интеграле приобретает вид
![]() .
.
Примеры
1. Вычислить интеграл 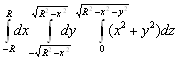 , перейдя к сферической системе координат.
, перейдя к сферической системе координат.
Область интегрирования есть верхняя половина шара с центром в начале координат и радиуса ![]() . Поэтому
. Поэтому ![]()
![]()
![]() . Далее,
. Далее, ![]()
![]() Следовательно,
Следовательно,

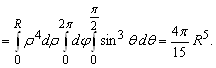
2. Вычислить интеграл  , перейдя к цилиндрической системе координат.
, перейдя к цилиндрической системе координат.
Область интегрирования есть половина кругового цилиндра радиуса 1, лежащая в полупространстве ![]() . Поэтому
. Поэтому ![]()
![]()
![]() . Следовательно,
. Следовательно,
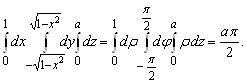
Задание 3.3
В двойном интеграле ![]() перейти к полярным координатам и расставить пределы интегрирования, если область
перейти к полярным координатам и расставить пределы интегрирования, если область ![]() задана неравенствами 1.
задана неравенствами 1. ![]() ;
;
2. ![]() ; 3.
; 3. ![]() ;
;
4.![]() ; 5.
; 5. ![]() ; 6.
; 6.![]() ; 7.
; 7. ![]() ; 8.
; 8. ![]() .
.
В тройном интеграле ![]() перейти к сферическим или цилиндрическим координатам и расставить пределы интегрирования, если область
перейти к сферическим или цилиндрическим координатам и расставить пределы интегрирования, если область ![]() задана неравенствами
задана неравенствами
9.![]() ;
;
10. ![]()
11. ![]() ;
;
12. ![]() .
.
Ответы:
1. 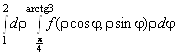 ; 2.
; 2.  ; 3.
; 3.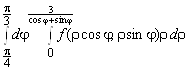 ; 4.
; 4.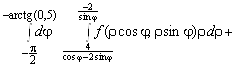
 ;
;
5. 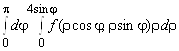 ; 6.
; 6. 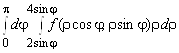 ; 7.
; 7.  ; 8.
; 8. 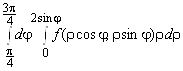 ;
;
9. сферические координаты,
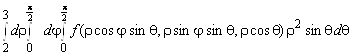
10. цилиндрические координаты,
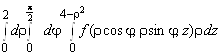 ;
;
11. цилиндрические координаты,
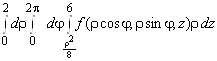 ;
;
12. цилиндрические координаты,
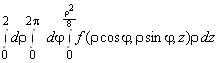 .
.
| < Предыдущая | Следующая > |
|---|