26. Замена переменных в интегралах

Теорема. Пусть - функция, заданная в области , - биективное (осуществляющее взаимно однозначное соответствие) дифференцируемое отображение,

.

Тогда

Где - модуль якобиана (определителя матрицы Якоби, или, что то же самое, производной матрицы ).

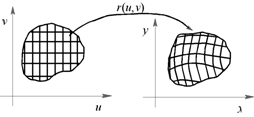Доказательство. Пусть . Тогда взаимно однозначное дифференцируемое отображение в можно записать в виде . Разобьём область на части прямыми параллельными координатным осям. Этому разбиению соответствует разбиение области кривыми . При этом прямоугольник с вершинами перейдёт в криволинейный четырёхугольник , ограниченный линиями .

Пусть - точка прямоугольника , , . Рассмотрим интегральную сумму

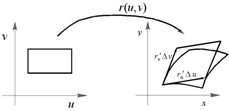Для вычисления интеграла от функции по области , в которой - площадь четырёхугольника . Из геометрического смысла производной , следует, что вектор является касательным к кривой в точке, а вектор будет касательным вектором кривой в той же точке. Далее,

, где и - бесконечно малые более высокого порядка малости, чем и . Можно показать, что площади криволинейного четырёхугольника и параллелограмма построенного на векторах , отличаются на бесконечно малую более высокого порядка малости, чем . Заметим, что если - линейное преобразование координат, то четырёхугольник совпадает с параллелограммом, построенным на векторах , . Поэтому заменим четырёхугольник указанным параллелограммом.. Его площадь равна . Вычисляя , получаем

Таким образом,

.

Переходя в последней сумме к пределу при увеличении числа разбиений, получаем вывод о справедливости теоремы в случае . Для доказательство аналогично, если заменить объём соответствующей элементарной области объёмом параллелепипеда, построенным на векторах

,,

,

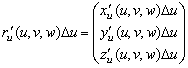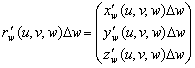Который равен или, что то же самое, модулю определителя матрицы Якоби (модулю якобиана) вектор-функции, отображающей в , умноженной на объём . В общем случае требуется замена меры Мерной элементарной области на меру Мерного параллелепипеда, которая равна модулю определителя матрицы Якоби (модулю определителя производной матрицы), умноженной на объём элементарной области в новых переменных. Теорема доказана.

Заметим, что для ортогональной системы координат на плоскости , где и - коэффициенты Ламе. Аналогично, в

Для полярной системы координат на плоскости матрица Якоби равна

.

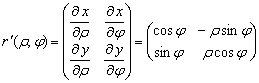Определитель этой матрицы равен , поэтому модуль Якобиана тоже равен и формула перехода к полярным координатам в двойном интеграле приобретает вид

< Предыдущая		Следующая >