25. Сферическая и цилиндрическая системы координат в
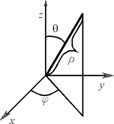 Возможны два обобщения полярной системы координат на случай пространства
Возможны два обобщения полярной системы координат на случай пространства ![]() . Первое из них называется сферической системой координат. Положение точки в этой сис-теме координат определяется длиной
. Первое из них называется сферической системой координат. Положение точки в этой сис-теме координат определяется длиной ![]() радиус-вектора точки, углом
радиус-вектора точки, углом ![]() между радиус-вектором точки и осью
между радиус-вектором точки и осью ![]() , углом
, углом ![]() между проекцией радиус-вектора точки на плоскость
между проекцией радиус-вектора точки на плоскость ![]() И осью
И осью ![]() Формулы перехода в координатной форме приобретают вид
Формулы перехода в координатной форме приобретают вид
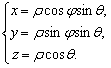
При этом ![]() . В векторной форме то же самое записывается в виде
. В векторной форме то же самое записывается в виде
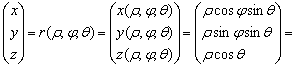
![]() .
.
Сферическая система координат является ортогональной. Действительно, вычисляя скалярное произведение векторов
![]() ,
,
![]() ,
,
![]() ,
,
Получаем требуемое. Коэффициенты Ламе для сферической системы координат равны ![]() ,
, ![]() ,
, ![]() .
.
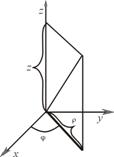 Второе обобщение полярной системы координат называется цилиндрической системой координат. Положение точки в этой системе координат определяется длиной
Второе обобщение полярной системы координат называется цилиндрической системой координат. Положение точки в этой системе координат определяется длиной ![]() проекции радиус-вектора точки на плоскость
проекции радиус-вектора точки на плоскость ![]() , углом
, углом ![]() между этой проекцией и осью
между этой проекцией и осью ![]() координатой
координатой ![]() . Формулы перехода в координатной форме приобретают вид
. Формулы перехода в координатной форме приобретают вид
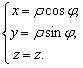
При этом ![]() . В векторной форме то же самое записывается в виде
. В векторной форме то же самое записывается в виде
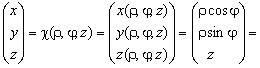
![]() .
.
Цилиндрическая система координат также ортогональна. Предлагается проверить это самим. Коэффициенты Ламе для цилиндрической системы координат равны ![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|