22. Вычисление тройных интегралов
Аналогично случаю двойного интеграла доказывается, что если ![]() - параллелепипед, то
- параллелепипед, то
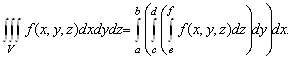
Пусть теперь ![]() - область, расположенная между плоскостями
- область, расположенная между плоскостями ![]() и для
и для ![]() область
область ![]() однозначно проектируется на плоскость
однозначно проектируется на плоскость ![]() и
и ![]() - эта проекция. Тогда
- эта проекция. Тогда
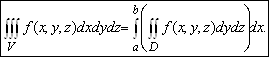
Если ![]() - цилиндр с образующими, параллельными оси
- цилиндр с образующими, параллельными оси ![]() , направляющей, лежащей в плоскости
, направляющей, лежащей в плоскости ![]() И являющейся границей области
И являющейся границей области ![]() , ограниченный поверхностями
, ограниченный поверхностями ![]()
![]() , то
, то 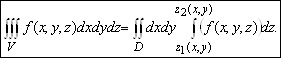
Примеры
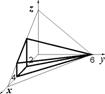
1. Пусть область ![]() ограничена поверхностями
ограничена поверхностями ![]()
![]()
![]() . В тройном интеграле
. В тройном интеграле ![]() перейти к повторным и расставить пределы интегрирования. Данная область есть цилиндр, ограниченный поверхностями
перейти к повторным и расставить пределы интегрирования. Данная область есть цилиндр, ограниченный поверхностями ![]() Проекция этого цилиндра на плоскость
Проекция этого цилиндра на плоскость ![]() Есть квадрат с границей
Есть квадрат с границей ![]()
![]()
![]()
![]() которая одновременно является направляющей цилиндра. Поэтому
которая одновременно является направляющей цилиндра. Поэтому

 2. Область
2. Область ![]() ограничена поверхностями
ограничена поверхностями ![]()
![]()
![]() В тройном интеграле
В тройном интеграле ![]() перейти к повторным и расставить пределы интегрирования. Область однозначно проектируется на треугольник
перейти к повторным и расставить пределы интегрирования. Область однозначно проектируется на треугольник ![]()
![]() лежащий в плоскости
лежащий в плоскости ![]() , являет
, являет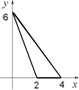 Ся цилиндром, ограниченным поверхностями
Ся цилиндром, ограниченным поверхностями ![]()
![]() направляющая которого есть указанный выше треугольник. Поэтому
направляющая которого есть указанный выше треугольник. Поэтому
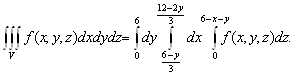
Задание 3.2
В тройном интеграле ![]() , перейти к повторным и расставить пределы интегрирования, если область
, перейти к повторным и расставить пределы интегрирования, если область ![]() задана неравенствами (приведён один из вариантов ответов).
задана неравенствами (приведён один из вариантов ответов).
1. ![]() ;
;
2. ![]()
3. ![]() ;
;
4. ![]() .
.
Ответы:
1. 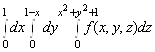 ; 2.
; 2. 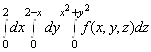 ;
;
3. 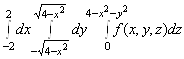 ; 4.
; 4.![]() .
.
| < Предыдущая | Следующая > |
|---|