21. Вычисление кратных интегралов. Вычисление двойных интегралов
Рассмотрим вначале самый простой случай прямоугольной области ![]() . Предположим, что для всякого
. Предположим, что для всякого ![]() существует интеграл
существует интеграл ![]() . Разобьём отрезки
. Разобьём отрезки ![]() и
и ![]() на части точками
на части точками ![]()
![]() Положим
Положим ![]() ,
, ![]() ,
, ![]() . Выберем на каждом из отрезков
. Выберем на каждом из отрезков ![]()
![]() по точке
по точке ![]() . При любых
. При любых ![]() и
и ![]() справедливо неравенство
справедливо неравенство
![]()
Интегрируя это неравенство по ![]() на отрезке
на отрезке ![]() , имеем
, имеем

Умножая последнее неравенство на ![]() и суммируя, получаем
и суммируя, получаем
 (3.1)
(3.1)
Заметим, что в левой и правой частях неравенства (3.1) стоят, соответственно, нижняя и верхняя суммы Дарбу для интеграла ![]() , которые могут быть введены так же, как и для определённого интеграла. В случае, когда функция
, которые могут быть введены так же, как и для определённого интеграла. В случае, когда функция ![]() непрерывна в области
непрерывна в области ![]() , то каждая из них совпадает с одной из интегральных сумм. Так как
, то каждая из них совпадает с одной из интегральных сумм. Так как 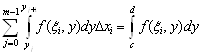 , то, переходя в неравенстве (3.1) к пределу, имеем, в случае интегрируемости функции
, то, переходя в неравенстве (3.1) к пределу, имеем, в случае интегрируемости функции ![]() ,
,

Последнее неравенство эквивалентно соотношению
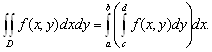
Аналогично, если существует ![]() , то
, то
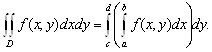
Обычно вместо  пишут
пишут ![]()
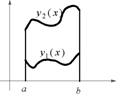
 Пусть теперь
Пусть теперь ![]() - криволинейная трапеция, ограниченная линиями
- криволинейная трапеция, ограниченная линиями ![]() и при этом выполнено неравенство
и при этом выполнено неравенство ![]() . Заключим эту область в прямоугольник
. Заключим эту область в прямоугольник ![]() , где
, где ![]() .
.
Положим
![]()
В силу построения ![]() получаем
получаем 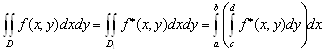 (3.2)
(3.2)
Далее, 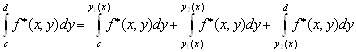 . Так как
. Так как 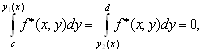 то (3.2) можно переписать в виде
то (3.2) можно переписать в виде
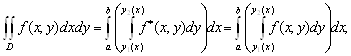

 Или, что то же самое,
Или, что то же самое,
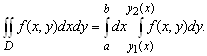 (3.3)
(3.3)

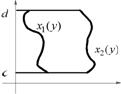 Для криволинейной трапеции, ограниченной линиями
Для криволинейной трапеции, ограниченной линиями ![]()
![]() (
(![]() для
для ![]() ) имеем
) имеем
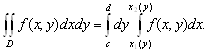 (3.4)
(3.4)
Интегралы, стоящие в правых частях формул (3.3) и (3.4), называются повторными, а результат о сведении кратного интеграла к одному из повторных носит название теоремы Фубини.
Примеры
 1. Пусть область
1. Пусть область ![]() - внутренность треугольника с вершинами
- внутренность треугольника с вершинами ![]() ,
, ![]() ,
, ![]() . Вычислить интеграл
. Вычислить интеграл ![]() . Перейдём к повторному интегралу типа (3.3) и расставим пределы интегрирования в нём. Найдём уравнения прямых
. Перейдём к повторному интегралу типа (3.3) и расставим пределы интегрирования в нём. Найдём уравнения прямых ![]() ,
, ![]() ,
, ![]() . Записывая уравнение прямой, проходящей через две точки, получаем уравнение прямой
. Записывая уравнение прямой, проходящей через две точки, получаем уравнение прямой ![]()
![]() или, что то же самое,
или, что то же самое, ![]() . Аналогично, для прямой
. Аналогично, для прямой ![]() :
: ![]() , или
, или![]() . Уравнение прямой
. Уравнение прямой ![]() имеет вид
имеет вид ![]() . Таким образом, область может быть задана неравенствами
. Таким образом, область может быть задана неравенствами ![]() ,
, ![]() . Поэтому
. Поэтому
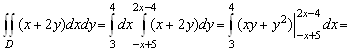
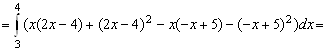
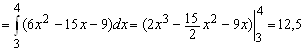
Для перехода к интегралу типа (3.4) требуется разбить область на две. Мы подобное проделаем в следующем примере, а читателю предлагаем в данном примере сделать это самостоятельно
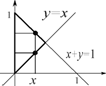 2. Пусть область
2. Пусть область ![]() задана неравенствами
задана неравенствами ![]()
![]() . В двойном интеграле
. В двойном интеграле ![]() перейти к повторным и расставить пределы интегрирования.
перейти к повторным и расставить пределы интегрирования.
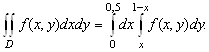
Перейдем вначале к повторному интегралу типа (3.3). Тогда ![]() . Поэтому
. Поэтому
Для перехода к интегралу типа (3.4) требуется разбить область на две: ![]() c границами
c границами ![]()
![]() и
и ![]() с границами
с границами ![]()
![]() . Поэтому
. Поэтому

 3. Пусть область
3. Пусть область ![]() - внутренность треугольника с вершинами
- внутренность треугольника с вершинами ![]() ,
, ![]() ,
, ![]() . В двойном интеграле
. В двойном интеграле ![]() перейти к повторным и расставить пределы интегрирования. Найдём уравнения прямых
перейти к повторным и расставить пределы интегрирования. Найдём уравнения прямых ![]() ,
, ![]() ,
, ![]() . Уравнение прямой
. Уравнение прямой ![]() можно записать в виде
можно записать в виде ![]() или, что то же самое, в форме
или, что то же самое, в форме ![]() ; прямой
; прямой ![]() в форме
в форме ![]() , или
, или![]() ; прямой
; прямой ![]() в виде
в виде ![]() , или
, или![]() . Как для перехода к интегралу вида (3.2), так и для перехода к интегралу вида (3.4) приходится разбивать область на две. Для интеграла вида (3.3) соответствующие области задаются неравенствами
. Как для перехода к интегралу вида (3.2), так и для перехода к интегралу вида (3.4) приходится разбивать область на две. Для интеграла вида (3.3) соответствующие области задаются неравенствами ![]() ,
, ![]() . Таким образом
. Таким образом
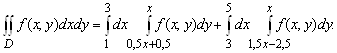
Расставить пределы интегрирования, взяв внешний интеграл по ![]() (то есть представить двойной интеграл в виде повторного интеграла вида (3.4)) предлагается самостоятельно.
(то есть представить двойной интеграл в виде повторного интеграла вида (3.4)) предлагается самостоятельно.
4. Пусть область ![]() задана неравенствами
задана неравенствами ![]() Тогда
Тогда 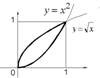
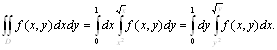
5. Изменить порядок интегрирования в интеграле
![]()
 Исходная область представлена в виде объединения двух областей
Исходная область представлена в виде объединения двух областей ![]() и
и ![]() . Таким образом, это область ограничена кривыми
. Таким образом, это область ограничена кривыми ![]() ,
, ![]() и
и ![]() . Её также можно задать неравенствами
. Её также можно задать неравенствами ![]() . Поэтому
. Поэтому 
Задание 3.1
В двойном интеграле ![]() , для заданной области
, для заданной области ![]() , перейти к повторным и расставить пределы интегрирования (приведены оба варианта ответа).
, перейти к повторным и расставить пределы интегрирования (приведены оба варианта ответа).
1. Область ![]() задана неравенствами а)
задана неравенствами а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д)![]() ; е)
; е)![]()
2. Область ![]() есть внутренность треугольника с вершинами а)
есть внутренность треугольника с вершинами а)![]() ,
, ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ,
, ![]() ; в)
; в) ![]() ,
, ![]() ,
, ![]() ; г)
; г) ![]() ,
, ![]() ,
, ![]() ;
;
3. Область ![]() есть внутренность четырёхугольника с вершинами
есть внутренность четырёхугольника с вершинами ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4. В повторном интеграле поменять порядок интегрирования.
А) ;
;
Б) 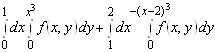 ;
;
В) ![]() .
.
Ответы:
1. а) 
 ; б)
; б) 
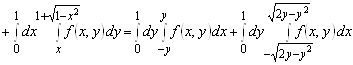 ;
;
В) 
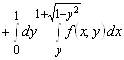 ; г)
; г) 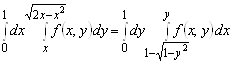 ;
;
Д) 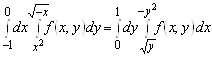 ;
;
Е) 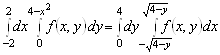
2. а) 
Б) 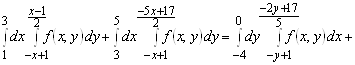
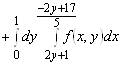 ; в)
; в) 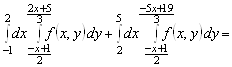
 ; г)
; г) 
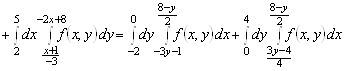 .
.
3. 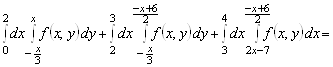
 .
.
4. а) 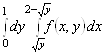 ; б)
; б)  ; в)
; в) ![]() .
.
| < Предыдущая | Следующая > |
|---|