20. Кратные интегралы. Определение и свойства

Пусть - некоторое множество. Диаметром Этого множества назовём число , где - расстояние между точками и .

Определение. Пусть функция определена и ограничена в области Разобьем область на части поверхностями размерности (на плоскости – кривыми, в – поверхностями и так далее), пронумеруем полученные элементарные области , выберем внутри каждой из них по точке и Составим сумму Где - мера области (на плоскости – площадь, в – объём и так далее). Предел полученных сумм по всевозможным разбиениям, если этот предел существует, не зависит от способа разбиения, способа выбора точек , при условии, Что максимальный из диаметров элементарных областей стремится к нулю, называется кратным интегралом от функции (двойным на плоскости, тройным в и так далее) и обозначается в общем случае, В и в , а функция называется интегрируемой по Риману.

Отметим некоторые свойства кратных интегралов при условии существования всех используемых ниже интегралов.

1. Если область разбита на две области , так, что и , пересекаются лишь по поверхности разбиения, то .

2..

3. .

Следующие ниже свойства справедливы для скалярнозначных функций.

4. Если для всех из , то .

5. Если для всех из , то.

6. .

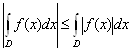7. Если , то

8. где - некоторое число такое, что .

9. Если Непрерывна в области , то существует точка из такая, что .

Аналогично тому, как это сделано при рассмотрении интеграла от функции одной переменной, можно рассмотреть нижние и верхние суммы Дарбу, нижний и верхний интегралы Дарбу и доказать следующие результаты.

Теорема 3.1. Интеграл от функции по области существует тогда и только тогда, когда нижний и верхний интегралы Дарбу равны между собой.

Теорема 3.2. Для всякой непрерывной на ограниченном замкнутом множестве функции существует интеграл по этой области.

Теорема 3.3. Если область можно разбить на конечное число областей, в замыкании каждой из которых функция непрерывна, то она интегрируема на этом множестве.

Определения ограниченного и замкнутого множеств можно найти в . Любознательным читателям предлагается доказать теоремы 3.1, 3.2, 3.3 самостоятельно, или посмотреть их доказательства в .

< Предыдущая		Следующая >