19. Вычисление длины дуги кривой

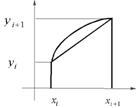Рассмотрим кривую . Разделим кривую на части точками Заменим дугу кривой между точками и хордой эти точки соединяющей. Тогда для длины дуги имеем . Просуммировав по всем точкам деления, получаем

Пусть кривая задана параметрически или, что то же самое, в векторной форме . Разделив отрезок точками получаем разбиение кривой точками . Тогда где - точка, лежащая между и . Просуммировав по всем точкам деления, получаем . Переходя в этой сумме к пределу при увеличении числа точек разбиения, имеем

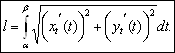(2.1)

Аналогично, для пространственной кривой, заданной параметрически 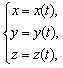или, что то же самое, в векторной форме 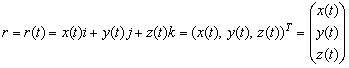, длина кривой равна

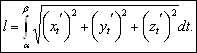(2.2)

Для кривой, заданной явно уравнением , формула (2.1) приобретает вид

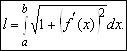(2.3)

Если кривая задана в полярной системе координат, то

Поэтому

Подставляя в формулу (2.1) для вычисления длины кривой, получаем

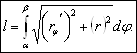(2.4)

Примеры

1. Найти длину дуги кривой , заключенной между точками Так как кривая задана явно, то 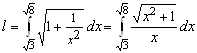. Делаем замену . Тогда и поэтому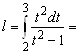

2. Найти длину дуги кривой заключенной между точами

Так как кривая задана параметрически, то и поэтому

.

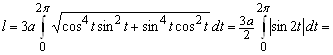
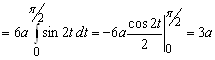3. Найти длину дуги кривой , заключенной между точками И Так как кривая задана в полярной системе координат, , то

.

Получился ожидаемый результат, так как уравнение , , определяет окружность радиуса 1 с центром в точке .

Задание 2.8

1. Найти площадь фигуры, ограниченной линиями , , ;

2. Найти площадь фигуры, ограниченной линиями , ;

3. Найти площадь фигуры, ограниченной линиями ,.

4. Трапеция ограничена кривыми . Найти объём тела, полученного вращением этой трапеции: а) вокруг оси ; б) вокруг оси .

5. Найти длину дуги кривой , заключенной между точками

6. Найти длину дуги кривой заключенной между точками .

7. Найти длину дуги кривой , заключенной между точками И .

Ответы: 1. ; 2. ; 3. ; 4. а) , б); 5. ; 6. ; 7. .

< Предыдущая		Следующая >