17. Приложения определённого интеграл. Вычисление площадей плоских фигур

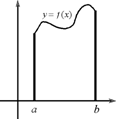Пусть для Рассмотрим криволинейную трапецию, ограниченную кривыми Разобьём отрезок на части точками , выберем внутри каждого элементарного отрезка по точке . Заменим криволинейную трапецию, ограниченную линиями , прямоугольником . Площадь этого прямоугольника равна и, если - непрерывная функция, то при достаточно малом близка площади заменяемой трапеции. Просуммировав, получим, с одной стороны, приближенное значение площади криволинейной трапеции, с другой стороны, интегральную сумму для интеграла . Переходя к пределу при увеличении числа точек разбиения, получаем площадь исходной криволинейной трапеции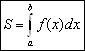

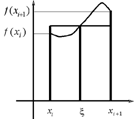Назовём трапецию простейшей областью, если она ограничена кривыми , и для всех выполнено неравенство . Нетрудно видеть, что для простейшей области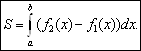

Аналогично, если для всех , то для криволинейной трапеции, ограниченной кривыми (простейшей области второго типа), имеем

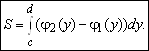
В общем случае плоскую область разбивают на простейшие области рассмотренных выше типов.

Примеры

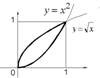1. Найти площадь фигуры, ограниченной линиями и . Эти кривые пересекаются в точках и . Поэтому

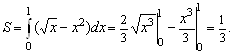
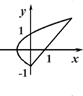2. Найти площадь фигуры, ограниченной линиями и . Эти кривые пересекаются в точках и . В данном случае лучше рассматривать простейшую область второго типа. Поэтому

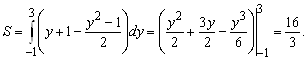
3. Найти площадь криволинейной трапеции, ограниченной линиями , , , . В данном случае

.

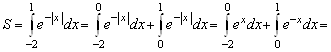
< Предыдущая		Следующая >