16. Несобственные интегралы второго рода
Если ![]() неограничена на
неограничена на ![]() , то особенность может быть в точках
, то особенность может быть в точках ![]() или внутренней точке этого отрезка. Мы рассмотрим случай с особенностью в точке
или внутренней точке этого отрезка. Мы рассмотрим случай с особенностью в точке ![]() .
.
Определение. Пусть ![]() задана на полуинтервале
задана на полуинтервале ![]() и
и ![]() Пусть далее для всякого
Пусть далее для всякого ![]() существует интеграл
существует интеграл ![]() Предел
Предел ![]() называется несобственным интегралом второго рода (интегралом от неограниченной функции) и обозначается
называется несобственным интегралом второго рода (интегралом от неограниченной функции) и обозначается ![]() Если
Если ![]() существует и конечен, то несобственный интеграл второго рода называется сходящимся, если же он не существует Или равен бесконечности, то несобственный интеграл второго рода называется расходящимся.
существует и конечен, то несобственный интеграл второго рода называется сходящимся, если же он не существует Или равен бесконечности, то несобственный интеграл второго рода называется расходящимся.
Аналогично определяются несобственные интегралы второго рода в случаях, когда подынтегральная функция бесконечно большая на нижнем пределе, во внутренней точке отрезка ![]() , на верхнем и нижнем пределах одновременно. Для удобства изложения мы рассматриваем случай особенности на верхнем пределе. Для остальных вариантов предлагается проделать это самостоятельно.
, на верхнем и нижнем пределах одновременно. Для удобства изложения мы рассматриваем случай особенности на верхнем пределе. Для остальных вариантов предлагается проделать это самостоятельно.
Примеры.
1. Рассмотрим ![]() . Пусть
. Пусть ![]() Тогда
Тогда ![]()
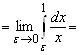
![]() Таким образом, рассмотренный интеграл при
Таким образом, рассмотренный интеграл при ![]() расходится. Пусть теперь
расходится. Пусть теперь ![]() Тогда
Тогда
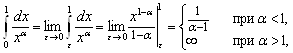
И мы окончательно получили, что рассматриваемый интеграл при ![]() сходится и при
сходится и при ![]() расходится. Аналогичные выводы можно сделать про несобственные интегралы
расходится. Аналогичные выводы можно сделать про несобственные интегралы 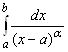 ,
,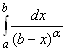 .
.
Интегралы ![]() ,
, ![]() ,
,  используются в признаке сравнения в качестве эталонных.
используются в признаке сравнения в качестве эталонных.
2. В интеграле 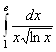 подынтегральная функция имеет особенность в точке
подынтегральная функция имеет особенность в точке ![]() , поэтому
, поэтому 
![]() .
.
Следовательно, интеграл сходится и его значение равно 2.
3. В интеграле ![]() подынтегральная функция имеет особенность в точках
подынтегральная функция имеет особенность в точках ![]() и
и ![]() , поэтому интеграл разбиваем на сумму двух, например,
, поэтому интеграл разбиваем на сумму двух, например, 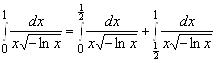 . Для первого из них
. Для первого из них 
![]() . Следовательно, интеграл расходится и поэтому исходный интеграл также расходится.
. Следовательно, интеграл расходится и поэтому исходный интеграл также расходится.
4. В интеграле 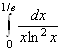 подынтегральная функция имеет особенность в точке
подынтегральная функция имеет особенность в точке ![]() , поэтому
, поэтому
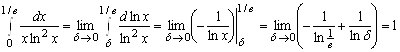 Следовательно, интеграл сходится и его значение равно 1.
Следовательно, интеграл сходится и его значение равно 1.
5. Выясним сходимость интеграла 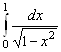 . Подынтегральная функция имеет особенность в точке
. Подынтегральная функция имеет особенность в точке ![]() . Поэтому
. Поэтому 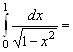
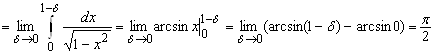
Следовательно, интеграл сходится и его значение равно ![]() .
.
6. Выяснить сходимость интеграла ![]()
Подынтегральная функция имеет особенность в точке ![]() . По определению имеем
. По определению имеем
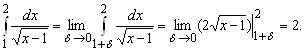
7. Выяснить сходимость интеграла ![]()
Подынтегральная функция имеет особенность в точке ![]() . По определению имеем
. По определению имеем
![]()
8. Выяснить сходимость интеграла ![]() .
.
Подынтегральная функция имеет особенность в точке ![]() . Поэтому разбиваем интеграл на сумму двух
. Поэтому разбиваем интеграл на сумму двух
![]() . Для первого из них имеем
. Для первого из них имеем
![]() .
.
Аналогично доказывается сходимость второго слагаемого. Следовательно исходный интеграл сходится.
Задание 2.6
Используя определение выяснить сходимость несобственных интегралов второго рода.
1.![]() ; 2.
; 2.![]() ; 3.
; 3. ; 4.
; 4.![]() ; 5.
; 5.![]() ; 6.
; 6. ![]() ; 7.
; 7. 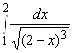 ; 8.
; 8. 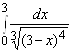 ; 9.
; 9. 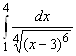 .
.
Ответы: 1.![]() ; 2. расходится; 3.
; 2. расходится; 3.![]() ; 4.
; 4.![]() ; 5.
; 5.![]() ; 6.
; 6. ![]() ; 7. расходится; 8. расходится; 9. расходится.
; 7. расходится; 8. расходится; 9. расходится.
Аналогично случаю несобственных интегралов первого рода формулируются и доказываются критерий Коши и признаки сравнения для несобственных интегралов второго рода.
Теорема 2.11.(Критерий Коши). Несобственный интеграл второго рода сходится тогда и только тогда, когда для всякого ![]() существует
существует ![]() Такое, что для всех
Такое, что для всех ![]() выполняется неравенство
выполняется неравенство 
Доказательство этого результата опустим.
Теорема 2.12. Пусть для всякого ![]() Выполнено неравенство
Выполнено неравенство ![]() . Тогда, если интеграл
. Тогда, если интеграл ![]() сходится, то интеграл
сходится, то интеграл ![]() сходится, а если интеграл
сходится, а если интеграл ![]() расходится, то интеграл
расходится, то интеграл ![]() расходится.
расходится.
Доказательство аналогично случаю несобственного интеграла первого рода.
Теорема 2.13. Если ![]() и
и ![]() - бесконечно большие одного порядка роста, то есть
- бесконечно большие одного порядка роста, то есть ![]() , то интегралы
, то интегралы ![]() И
И![]() либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Доказательство аналогично случаю несобственного интеграла первого рода.
Примеры
1. Для интеграла  подынтегральная функция имеет особенность в точках
подынтегральная функция имеет особенность в точках ![]() и
и ![]() . Точки
. Точки ![]() в промежуток интегрирования не входят. Поэтому, находя порядок роста этой функции относительно
в промежуток интегрирования не входят. Поэтому, находя порядок роста этой функции относительно ![]() , имеем
, имеем

Таким образом, порядок роста равен 0,5 и интеграл сходится.
2. В интеграле 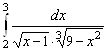 подынтегральная функция имеет особенность в точках
подынтегральная функция имеет особенность в точках ![]() и
и ![]() . Точки
. Точки ![]() и
и ![]() в промежуток интегрирования не входят. Поэтому, находя порядок роста этой функции относительно
в промежуток интегрирования не входят. Поэтому, находя порядок роста этой функции относительно ![]() , имеем
, имеем ![]()
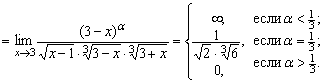
Таким образом, порядок роста равен ![]() и интеграл сходится.
и интеграл сходится.
3. Выясним сходимость интеграла  .
.
Подынтегральная функция имеет особенность в точке ![]() . Находя порядок роста этой функции относительно
. Находя порядок роста этой функции относительно ![]() , имеем
, имеем

Таким образом, порядок роста равен 1,5 и интеграл расходится.
4. В интеграле  подынтегральная функция имеет особенность в точке
подынтегральная функция имеет особенность в точке ![]() . Находя порядок роста этой функции относительно
. Находя порядок роста этой функции относительно ![]() , имеем
, имеем
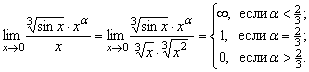
Таким образом, порядок роста равен ![]() И интеграл сходится.
И интеграл сходится.
5. Выясним сходимость интеграла 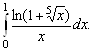
Подынтегральная функция имеет особенность в точке ![]() . Находя порядок роста этой функции относительно
. Находя порядок роста этой функции относительно ![]() , имеем
, имеем 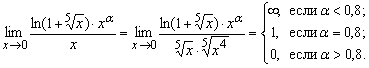
Таким образом, порядок роста равен ![]() И интеграл сходится.
И интеграл сходится.
6. В интеграле 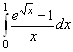 подынтегральная функция имеет особенность в точке
подынтегральная функция имеет особенность в точке ![]() . Находя порядок роста этой функции относительно
. Находя порядок роста этой функции относительно ![]() , имеем
, имеем

Таким образом, порядок роста равен ![]() И интеграл сходится.
И интеграл сходится.
7. Выяснить сходимость интеграла ![]()
Подынтегральная функция имеет особенность в точках ![]() и
и ![]() Обе входят в промежуток интегрирования. Разбиваем интеграл на два
Обе входят в промежуток интегрирования. Разбиваем интеграл на два
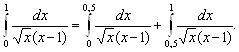
Первый из этих интегралов сходится, так как порядок роста подынтегральной функции при ![]() относительно
относительно ![]() равен
равен ![]() , а второй расходится, так как порядок роста подынтегральной функции при
, а второй расходится, так как порядок роста подынтегральной функции при ![]() относительно
относительно ![]() равен 1. Поэтому интеграл расходится.
равен 1. Поэтому интеграл расходится.
Задание 2.7
Используя теорему сравнения выяснить сходимость несобственных интегралов. В ответе указаны: точка, в которой функция бесконечно большая; порядок роста подынтегральной функции относительно пробной функции; сходимость.
1. 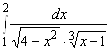 ; 2.
; 2. 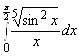 ; 3.
; 3. ![]() ;
;
4. ![]() ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ;
;
8. 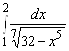 ; 9.
; 9. 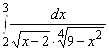 ; 10.
; 10. 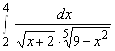 .
.
Ответы: 1. ![]() ,
, ![]() , сходится; 2.
, сходится; 2. ![]()
![]() , сходится; 3.
, сходится; 3. ![]() ,
, ![]() , сходится; 4.
, сходится; 4.![]()
![]() , сходится; 5.
, сходится; 5. ![]()
![]() , расходится; 6.
, расходится; 6. ![]() ,
, ![]() , сходится; 7.
, сходится; 7. ![]()
![]() , сходится; 8.
, сходится; 8. ![]()
![]() , сходится; 9.
, сходится; 9. ![]()
![]() ,
, ![]()
![]() , сходится; 10.
, сходится; 10. ![]()
![]() , сходится;
, сходится;
| < Предыдущая | Следующая > |
|---|