09. Интегрирование простейших иррациональностей и выражений, содержащих тригонометрические функции
Рациональной функцией переменных ![]() назовём отношение двух полиномов от этих переменных, или, что тоже самое, отношение двух линейных комбинаций целых степеней этих переменных.
назовём отношение двух полиномов от этих переменных, или, что тоже самое, отношение двух линейных комбинаций целых степеней этих переменных.
Пусть ![]() – рациональная функция от
– рациональная функция от ![]() Эта функция, а следовательно, и интеграл от неё, рационализируется подстановкой
Эта функция, а следовательно, и интеграл от неё, рационализируется подстановкой ![]() Где
Где ![]() – наименьшее общее кратное чисел
– наименьшее общее кратное чисел ![]() . Тогда
. Тогда ![]() и под интегралом стоит рациональная функция от
и под интегралом стоит рациональная функция от ![]() Аналогично, если подынтегральное выражение
Аналогично, если подынтегральное выражение ![]() есть рациональная функция от
есть рациональная функция от ![]() , то подынтегральная функция рационализируется подстановкой
, то подынтегральная функция рационализируется подстановкой ![]() где
где ![]() – наименьшее общее кратное чисел
– наименьшее общее кратное чисел ![]() . Тогда
. Тогда ![]() Подставляя в исходное выражение, получаем рациональную функцию от
Подставляя в исходное выражение, получаем рациональную функцию от ![]()
Примеры.
1. Вычислить ![]() Наименьшее общее кратное чисел 2 и 3 равно 6. Поэтому делаем замену
Наименьшее общее кратное чисел 2 и 3 равно 6. Поэтому делаем замену ![]() Тогда
Тогда ![]() и
и
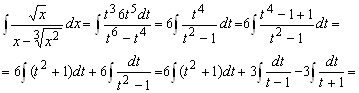
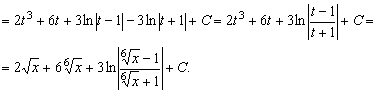
2. Вычислить 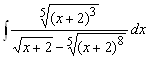 . Наименьшее общее кратное чисел 2 и 5 равно 10. Поэтому делаем замену
. Наименьшее общее кратное чисел 2 и 5 равно 10. Поэтому делаем замену ![]() Тогда
Тогда ![]() И
И

3. 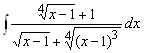 Наименьшее общее кратное чисел 2 и 4 равно 4. Поэтому делаем замену
Наименьшее общее кратное чисел 2 и 4 равно 4. Поэтому делаем замену ![]() Тогда
Тогда ![]() и
и
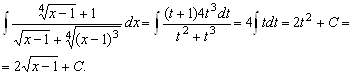
Для интегрирования рациональных функций вида ![]() применяют подстановку
применяют подстановку ![]() , которая называется универсальной тригонометрической подстановкой. Тогда
, которая называется универсальной тригонометрической подстановкой. Тогда ![]() К сожалению, универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками. Если
К сожалению, универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками. Если ![]()
![]() , то делают замену
, то делают замену ![]() и тогда
и тогда ![]() При
При ![]() , полагают
, полагают ![]() при этом
при этом ![]() а в случае
а в случае ![]()
![]() делают замену
делают замену ![]() , при которой
, при которой ![]() ,
, ![]() , или
, или ![]() . Проиллюстрируем сказанное примерами.
. Проиллюстрируем сказанное примерами.
Примеры
1. Вычислить интеграл ![]() .
.
Делаем замену ![]() . Тогда
. Тогда ![]()
![]()
![]()
2. Вычислить интеграл ![]() .
.
Делая замену ![]() , получаем
, получаем
![]()
![]()
3. Найти интеграл ![]() .
.
Делаем замену ![]() Подставляя, получаем
Подставляя, получаем
![]()
![]()
Заметим, что в данном примере лучше было сделать замену ![]() , так как эта подстановка быстрее приводит к цели. Действительно, тогда
, так как эта подстановка быстрее приводит к цели. Действительно, тогда ![]() и поэтому
и поэтому ![]()
![]() .
.
4. Вычислить интеграл ![]() .
.
Делаем замену ![]() . Тогда
. Тогда ![]()
![]()
![]()
5. Вычислить интеграл ![]() .
.
Делая замену ![]() , получаем
, получаем
![]()
![]() .
.
6. Найти интеграл ![]() .
.
Делаем замену ![]() Подставляя, получаем
Подставляя, получаем
![]()
![]() .
.
![]()
![]()
![]() Для интегрирования рациональных выражений вида
Для интегрирования рациональных выражений вида ![]() применяют замену
применяют замену ![]() или
или ![]() , выражений вида
, выражений вида ![]() - подстановку
- подстановку ![]() или
или ![]() , а для интегрирования выражений вида
, а для интегрирования выражений вида ![]() применяют замену
применяют замену ![]() или
или ![]() . Возможно в этих случаях пользоваться так же заменами с гиперболическими функциями.
. Возможно в этих случаях пользоваться так же заменами с гиперболическими функциями.
Примеры
1. Для вычисления интеграла ![]() воспользуемся заменой
воспользуемся заменой ![]() . Тогда
. Тогда ![]()
![]() и исходный интеграл равен интегралу
и исходный интеграл равен интегралу ![]() . Тогда
. Тогда ![]() Делая обратную замену
Делая обратную замену ![]() , получаем
, получаем ![]()
![]() . После преобразований получаем
. После преобразований получаем 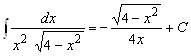 .
.
2. Для вычисления интеграла ![]() воспользуемся заменой
воспользуемся заменой ![]() . Тогда
. Тогда ![]()
![]() и исходный интеграл равен интегралу
и исходный интеграл равен интегралу ![]() . Тогда
. Тогда ![]() Делая обратную замену
Делая обратную замену ![]() , получаем
, получаем ![]()
![]() . После преобразований получаем
. После преобразований получаем 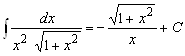 .
.
Задание 1.5
Вычислить интегралы:
1. 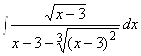 ; 2.
; 2. 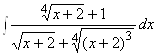 ;
;
3. ![]() ; 4.
; 4. ![]() ; 5.
; 5. ![]() ;
;
6. ![]() ; 7.
; 7. ![]() ; 8.
; 8. ![]() .
.
Ответы: 1. 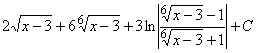 ;
;
2. ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() ;
;
5. ![]() ; 6.
; 6. ![]() ;
;
7.![]() ; 8.
; 8. ![]() .
.
| < Предыдущая | Следующая > |
|---|