08. Интегрирование рациональных дробей
Рациональной дробью или рациональной функцией называется отношение двух полиномов (многочленов), то есть выражение вида ![]() , где
, где
![]()
и
![]() -
-
Полиномы (многочлены) степеней K и N соответственно. Если степень полинома (многочлена) в числителе меньше степени полинома в знаменателе, то есть ![]() то такую рациональную дробь называют правильной.
то такую рациональную дробь называют правильной.
В дальнейшем будем считать, что ![]() , так как в противном случае всегда можно представить числитель в виде
, так как в противном случае всегда можно представить числитель в виде ![]() где
где ![]() И
И ![]() -полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома
-полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома ![]() меньше N. Тогда
меньше N. Тогда
![]() , (1.2)
, (1.2)
А интеграл от полинома ![]() Мы вычислять умеем.
Мы вычислять умеем.
Покажем на примере, как можно получить разложение (1.2). Пусть
![]()
![]() Разделим полином
Разделим полином ![]() На полином
На полином ![]() Так же, как мы делим вещественные числа. Имеем
Так же, как мы делим вещественные числа. Имеем
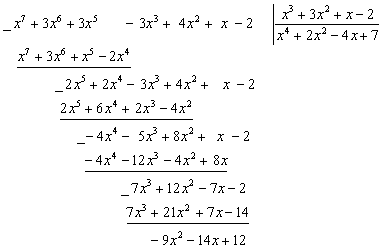
Таким образом, мы получили целую часть дроби (частное от деления полинома ![]() На полином
На полином ![]() )
) ![]() и остаток
и остаток ![]() от этого деления. Поэтому можем записать
от этого деления. Поэтому можем записать ![]()
![]() .
. ![]()
Простейшими рациональными дробями назовём дроби ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Рассмотрим интегрирование этих дробей. Интегралы ![]() ,
, ![]() ,
, ![]() являются табличными, а интеграл
являются табличными, а интеграл ![]() может быть найден или по рекуррентной формуле (1.1)
может быть найден или по рекуррентной формуле (1.1) ![]() полученной выше интегрированием
полученной выше интегрированием ![]() по частям, или с помощью таблиц
по частям, или с помощью таблиц ![]() . Интегралы
. Интегралы ![]() ,
, ![]() в случае, когда знаменатель имеет комплексные корни (дискриминант
в случае, когда знаменатель имеет комплексные корни (дискриминант ![]() ), сводятся, с помощью выделения полного квадрата, к интегралам
), сводятся, с помощью выделения полного квадрата, к интегралам ![]() ,
, ![]() заменой
заменой ![]() . Наконец, как это указывалось ранее, интегралы
. Наконец, как это указывалось ранее, интегралы ![]() ,
, ![]() выделением в числителе дифференциала выражения
выделением в числителе дифференциала выражения ![]() Сводятся к интегралам
Сводятся к интегралам ![]() ,
, ![]() .
.
Таким образом, осталось научиться раскладывать правильные рациональные дроби на сумму простейших.
По основной теореме алгебры [6] любой полином может быть разложен на простейшие множители, то есть представлен в виде ![]() , где
, где ![]() –действительные или комплексные корни полинома
–действительные или комплексные корни полинома ![]() , повторенные столько раз, какова их кратность.
, повторенные столько раз, какова их кратность.
Пусть полином ![]() имеет
имеет ![]() различных корней
различных корней ![]() . Тогда правильная рациональная дробь может быть представлена в виде
. Тогда правильная рациональная дробь может быть представлена в виде ![]() , где
, где ![]() - числа, подлежащие определению. Если
- числа, подлежащие определению. Если ![]() - корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых
- корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых ![]() . Если
. Если ![]() - комплексный корень кратности
- комплексный корень кратности ![]() Полинома с действительными коэффициентами, то комплексно сопряженное число
Полинома с действительными коэффициентами, то комплексно сопряженное число ![]() - тоже корень кратности
- тоже корень кратности ![]() этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида
этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида ![]() если
если ![]() – корни кратности один. Если
– корни кратности один. Если ![]() – корни кратности
– корни кратности ![]() , то им соответствует
, то им соответствует ![]() Слагаемых и соответствующее разложение имеет вид
Слагаемых и соответствующее разложение имеет вид
![]() .
.
Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей рассмотренных в начале пункта.
Одним из способов нахождения коэффициентов ![]() в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами
в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами ![]() приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях
приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях ![]() (так как полиномы равны, если равны коэффициенты при одинаковых степенях
(так как полиномы равны, если равны коэффициенты при одинаковых степенях ![]() ), получаем систему линейных уравнений для определения этих коэффициентов. Продемонстрируем изложенное на примерах.
), получаем систему линейных уравнений для определения этих коэффициентов. Продемонстрируем изложенное на примерах.
Примеры
1. Найти ![]() .
.
Корни знаменателя – ![]() кратности 1 и
кратности 1 и![]() кратности 2. Поэтому
кратности 2. Поэтому ![]()
![]() и подынтегральная функция может быть представлена в виде
и подынтегральная функция может быть представлена в виде
![]()
Приводя к общему знаменателю, получаем

Приравнивая коэффициенты при одинаковых степенях ![]() в числителях правой и левой частей последнего сотношения, получаем
в числителях правой и левой частей последнего сотношения, получаем

Решая эту систему, находим ![]() .
.
Таким образом,
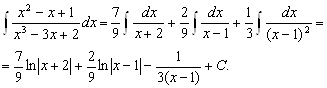
2. Найти ![]() .
.
Корни знаменателя – ![]() кратности 1 и два комплексных корня
кратности 1 и два комплексных корня![]() . Поэтому
. Поэтому ![]() и подынтегральная функция может быть представлена в виде
и подынтегральная функция может быть представлена в виде
![]()
Приводя к общему знаменателю, получаем
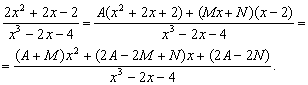
Приравнивая коэффициенты при одинаковых степенях ![]() в числителях правой и левой частей последнего сотношения, получаем
в числителях правой и левой частей последнего сотношения, получаем
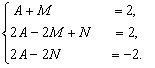
Решая эту систему, находим ![]()
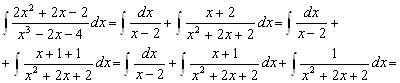
Таким образом,
![]()
3. Найти ![]() .
.
Корни знаменателя ![]() кратности 2 и пара комплексно сопряжённых корней
кратности 2 и пара комплексно сопряжённых корней ![]() кратности 1. Поэтому подынтегральная функция может быть представлена в виде
кратности 1. Поэтому подынтегральная функция может быть представлена в виде
![]() .
.
Приводя к общему знаменателю и подобные, получаем
 Приравнивая коэффициенты при одинаковых степенях
Приравнивая коэффициенты при одинаковых степенях ![]() в числителях правой и левой частей последнего сотношения, получаем
в числителях правой и левой частей последнего сотношения, получаем
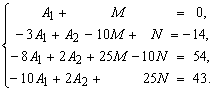
Решая эту систему, находим ![]() .
.
Таким образом,
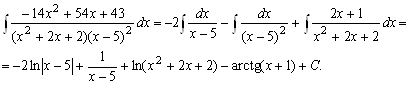 4. Найти
4. Найти ![]() .
.
Корни знаменателя – ![]() кратности 1 и два комплексных корня
кратности 1 и два комплексных корня![]() кратности 2. Поэтому подынтегральная функция может быть представлена в виде
кратности 2. Поэтому подынтегральная функция может быть представлена в виде
![]()
Дальнейшие вычисления предлагается проделать самостоятельно.
Задание 1.4
Вычислить интегралы:
1.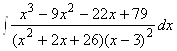 ; 2.
; 2.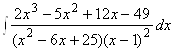 .
.
Написать разложение рациональной дроби на элементарные (не находя коэффициентов).
3. ; 4.
; 4. .
.
Ответы:
1. ![]() ;
;
2. ![]() .
.
3.![]() ;
;
4.![]() .
.
| < Предыдущая | Следующая > |
|---|