06. Интегрирование по частям

Пусть И - дифференцируемые функции. Тогда Поэтому Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что , получаем сотношение

Называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

Примеры

1. Вычислить

Положим Тогда , , и в качестве можем взять . Поэтому

2. Вычислить.

Полагаем Тогда , , и в качестве можем взять . Следовательно

3. Вычислить . Полагаем Тогда , , и в качестве можем взять , поэтому .

При использовании формулы интегрирования по частям нужно удачно выбрать И , чтобы интеграл, полученный в правой части формулы, находился легче. Положим в первом примере Тогда и Вряд ли интеграл можно считать проще исходного. Основные рекомендации здесь такие.

Если подынтегральная функция есть произведение полинома (многочлена) на экспоненту () или тригонометрическую функцию, то обычно в качестве выбирают полином, а всё остальное относят к .

Заметим, что иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла . Полагаем Тогда , и . Для вычисления второго слагаемого снова применяем формулу интегрирования по частям, полагая Тогда , , и поэтому . Таким образом, .

Интеграл Предлагается найти самостоятельно.

Приведём ещё несколько примеров на применение формулы интегрирования по частям.

4. Вычислить . Полагаем Тогда , и в качестве можем взять . Поэтому

5. Вычислить . Полагаем , . Тогда и . Для нахожления второго слагаемого снова применяем формулу интегрирования по частям, полагая . Тогда 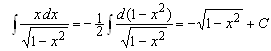и в качестве можно взять . Таким образом, окончательно получаем

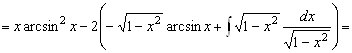
6. Вычислить . Полагаем

. Тогда и . Полагая во втором слагаемом , имеем , поэтому в качестве можно взять и, следовательно,

Окончательно

7. Вычислить . Полагаем . Тогда и поэтому . Применяя ко второму слагаемому формулу интегрирования по частям с , имеем . Поэтому .

8. Вычислить . Полагаем . Тогда и поэтому . Применяя ко второму слагаемому формулу интегрирования по частям с , имеем . Поэтому

9. Вычислить . Полагаем , . Тогда и поэтому 10. Интеграл вычисляется либо интегрированием по частям с , либо с помощью замены переменной . В первом случае и поэтому

Во втором случае и поэтому

С помощью интегрирования по частям вычисляется пятый интеграл в контрольной работе 5 (примеры 1-9). Шестой интеграл находится аналогично примеру 10.

11. Вычислим интеграл . Положив , получаем . Применив к интегралу в правой части формулу интегрирования по частям с , имеем . Разрешая последнее равенство относительно , получаем

Таким образом нами, в частном случае , доказана формула 16 из таблицы интегралов. Интеграл примера 11, равно как и интегралы , , называется циклическим. Циклические интегралы вычисляются по схеме примера 11. Предлагается вывести формулы для вычисления этих интегралов самостоятельно или ознакомиться с их получением, например, в [5].

12. С помощью формулы интегрирования по частям найдём . Положив , получаем

Из крайних частей последнего равенства, разрешая относительно , получаем рекуррентную формулу

(1.1)

Для вычисления интеграла при любом . Действительно, . Тогда . Аналогично находятся , и так далее. По приведённой схеме эти интегралы получены в таблицах интегралов и других.