05. Таблица основных дифференциалов

1. , где и - некоторые числа. В частности, и так далее.

2. . В частности, , , , , .

3. .

4. .

5..

6. .

7. .

8. .

9. .

10. .

Остальное читатель в состоянии восстановить самостоятельно из таблицы производных.

Покажем теперь применение вышесказанного для некоторых интегралов с указанием табличных, к которым они сводятся.

Интегралы :

. В этом месте можно либо продолжить вычисления непосредственно и тогда получим , либо сделать замену переменных и тогда .

;

;

Интегралы :

Знак модуля опущен в силу того, что 1 + X2 ³ 1 > 0 для всех X из R.

.

;

;

Интегралы : ;;

;

;

;

;

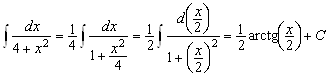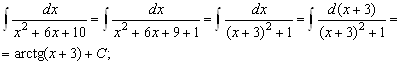
Для интеграла имеем

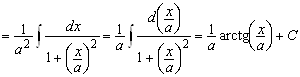. Таким образом нами доказана формула 5а таблицы интегралов. Часть из приведённых выше примеров можно сделать используя эту формулу.

Интегралы : ;

; ;

;

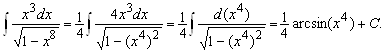
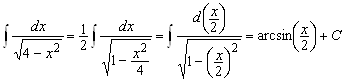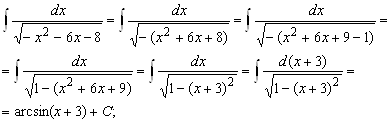
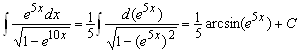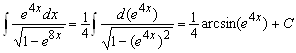Для интеграла имеем

. Таким образом нами доказана формула 6а таблицы интегралов. Часть из приведённых выше примеров можно сделать используя эту формулу.

Интегралы :

;

; ;

Интегралы .

;

;

Интегралы .

;

;

;

С помощью рассмотренного приёма вычисляются первые четыре интеграла в контрольной работе 5.

Задание 1.1.

Найти интегралы:

1. ; 2. ; 3. ;

4. ; 5. ; 6. ; 7.; 8. ; 9. ; 10. ; 11. ; 12.; 13.;

14. ; 15. ; 16. ; 17. ; 18. ; 19. ; 20. ;

21. ; 22. ; 23. ;

24. ; 25 ;

Ответы: 1. ; 2. ;

3.; 4. ; 5. ;

6. ; 7.; 8. ;

9. ; 10. ; 11. ; 12.; 13. ; 14. ; 15. ; 16. ; 17. ;

18. ; 19. ; 20. ;

21. ; 22. ; 23. ;

24. ; 25 ;

< Предыдущая		Следующая >