3.2. Решение задач

Пример 1. В некоторой точке C линии AB длины L произошел разрыв. Какова вероятность того, что точка C удалена от точки A на расстояние не меньше ?

Решение. Расположим отрезок AB на числовой оси Ox так, как изображено на рис. 2.

Рис. 2

Пусть x – координата случайной точки C отрезка AB, . Ясно, что исходов опыта (разрыв линии AB в точке C) бесчисленное множество и все они равновозможны. На отрезке AB возьмем точку M, расстояние которой от точки A, равно .

Очевидно, что событие A={точка C удалена от точки A на расстояние не меньше } произойдет, если точка C попадет на отрезок MB=[,L].

Таким образом, областью, благоприятствующей наступлению события A (на рис. 2 она заштрихована), является отрезок MB, а множеству исходов опыта соответствует отрезок AB=[0,L].

Тогда по формуле (3)

.

Пример 2. (Задача о встрече). Два студента A и B условились встретиться в определенном месте во время перерыва между 13 ч и 13 ч 50 мин. Пришедший первым ждет другого в течение 10 мин., после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанных 50 минут может произойти наудачу и моменты прихода независимы?

Решение. Пусть x – время прихода студента A, а y – студента B. Ясно, что , .

Будем рассматривать x и y как декартовы координаты на плоскости Oxy, выбрав в качестве единицы масштаба одну минуту. Тогда все возможные исходы изобразятся точками квадрата со стороной a=50, т. е. .

Интересующее нас событие C={студенты A и B встретятся} наступит тогда и только тогда, если разность между моментами их прихода будет не более 10 минут (по модулю), т. е. .

Неравенство , т. е. определяет благоприятствующую событию C область g, заштрихованную на рис.3.

Тогда по формуле (2) искомая вероятность равна

.

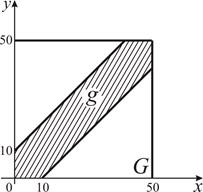
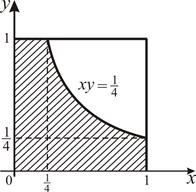
Рис. 3 Рис. 4

Пример 3. Какова вероятность того, что произведение двух наугад взятых правильных положительных дробей будет не больше ?

Решение. Обозначим через x и y соответственно две положительные правильные дроби. Ясно, что 0<x<1, 0<y<1. Будем рассматривать x и y как декартовы координаты на плоскости. Всевозможные исходы изобразятся

На плоскости точками (x, y) квадрата со стороной, равной 1. Поэтому область G={(x, y): 0<x<1, 0<y<1}. Интересующее нас событие A={произведение двух положительных дробей будет не больше } наступит тогда и только тогда, когда будет выполнено условие . Это неравенство определяет благоприятствующую событию A область g, заштрихованную на рис.4. Учитывая, что , а 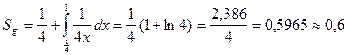, согласно формуле (2) найдем .

< Предыдущая		Следующая >