3.1. Геометрическая вероятность
В классическом определении вероятности рассматривается полная группа Конечного числа равновероятных событий. На практике же очень часто встречаются испытания с Бесконечным (вообще говоря, несчетным) Числом возможных исходов, поэтому в таких случаях классическое определение вероятности неприменимо. Тогда вводят понятие Геометрической вероятности, т. е. вероятности попадания точки в область (отрезок, часть плоскости, часть тела и т. д.).
Рассмотрим, например, на плоскости некоторую область G, имеющую площадь ![]() , и внутри области G область g с площадью
, и внутри области G область g с площадью ![]() . Пусть в область G наудачу бросается точка. При этом попадание точки в область G – достоверное событие, а в g – случайное. Предполагается, что все точки области G Равноправны, т. е. наудачу брошенная точка может попасть в любую точку области G, и вероятность события A – попадания точки в область g – пропорциональна площади этой области и не зависит от ее расположения и формы (рис.1).
. Пусть в область G наудачу бросается точка. При этом попадание точки в область G – достоверное событие, а в g – случайное. Предполагается, что все точки области G Равноправны, т. е. наудачу брошенная точка может попасть в любую точку области G, и вероятность события A – попадания точки в область g – пропорциональна площади этой области и не зависит от ее расположения и формы (рис.1).
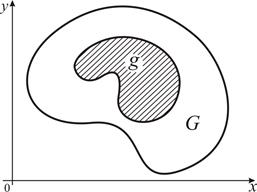
Рис. 1
Геометрической вероятностью события A называется отношение площади области g к площади области G, т. е.
![]() (2)
(2)
Область g называется Благоприятствующей (благоприятной) событию A.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, можно записать
![]() (3)
(3)
| < Предыдущая | Следующая > |
|---|