4.2. Огибающая однопараметрического семейства поверхностей
Определение огибающей семейства поверхностей не отличается по сути от определения огибающей семейства кривых.
Пусть имеется семейство поверхностей
![]() . (4.5)
. (4.5)
Фиксируя значение С, получим определенную поверхность семейства. Рассмотрим новую поверхность, которая определяется тем же уравнением, но с переменной величиной С
![]() ,
,
И пусть этот переменный параметр определяется из соотношения
![]() .
.
Можно сказать, что эта поверхность определяется системой уравнений
![]() ,
, ![]() . (4.6)
. (4.6)
Покажем, что эта система определяет огибающую данного семейства поверхностей, т. е. поверхность, которая в каждой своей точке касается какой-либо поверхности семейства. Действительно, для заданного семейства (48) в силу постоянности С должно выполняться условие
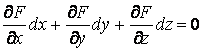 .
.
На огибающей поверхности С – переменная величина, и мы должны записать
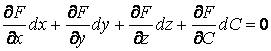 .
.
В силу условия ![]() для огибающей эти два условия совпадают, т. е. бесконечно малое перемещение (
для огибающей эти два условия совпадают, т. е. бесконечно малое перемещение (![]() ) в общих точках огибающей и поверхности семейства ортогонально одному и тому же направлению, которое определяется вектором
) в общих точках огибающей и поверхности семейства ортогонально одному и тому же направлению, которое определяется вектором  , откуда и следует доказательство искомого касания.
, откуда и следует доказательство искомого касания.
Заметим, что огибающая семейства поверхностей может и не существовать.
Пример. Рассмотрим семейство сфер заданного радиуса ![]() , центры которых находятся на оси
, центры которых находятся на оси ![]()
![]() .
.
Дифференцируя по С, имеем ![]() . Исключая из этих уравнений С, получим уравнение кругового цилиндра
. Исключая из этих уравнений С, получим уравнение кругового цилиндра
![]() ,
,
Который касается каждой из сфер данного семейства.
| < Предыдущая | Следующая > |
|---|